Запись означает, что a меньше, чем b;запись означает, что a больше, чем b.запись означает, что a не равно b.Эти математические отношения называются строгим неравенством. В противоположность им нестрогие неравенства означают следующее:запись означает, что a меньше либо равно b;запись означает, что a больше либо равно b.Кроме того, иногда требуется показать, что одна из величин много больше другой, обычно на несколько порядков:запись означает, что a намного больше b.Иногда не требуется знать результат и тогда можно определить формальное неравенство как два числа или алгебраических выражения, соединённые знаками >,<,≠.Неравенство называется точным, если его нельзя улучшить.Например является точным, а нет.Неравенства, содержащие неизвестные величины, подразделяются на: неравенства подразделяются на неравенства первой, второй, и т. д. степени.Пример:Неравенство — алгебраическое, первой степени.Неравенство — алгебраическое, второй степени.Неравенство — трансцендентное.
1) 1-3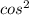
x=2sin(x)cos(x)
единицу представим по тригонометрическому тождеству:1=sin²x+cos²x
sin²x+cos²x-3cos²x-2sin(x)cos(x)=0
sin²x-2sin(x)cos(x)-2cos²x=0
делим каждый член уравнения на cos²x
tg²x-2tgx-2=0
решаем квадратное уравнение
D=12
tgx₁=1+√3 tgx₂=1-√3
x₁=arctg(1+√3)+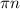
x₂=arctg(1-√3)+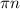
2) 3Sin²x+2SinxCosx=2
3Sin²x+2SinxCosx=2(Sin²x+Cos²x)
Sin²x+2SinxCosx-2Cos²x=0
Уравнение однородное 2 степени. Разделим его на Cos²x
Tg²x+2Tgx-2=0
Tgx=y
y²+2y-2=0
D=12>0
y=(-2+2√3)/2=-1+√3 или y=(-2-2√3)/2= -1-√3
Tgx=-1+√3⇒ x=arctg(-1+√3)+πn,n∈Z
Tgx= -1-√3 ⇒x= arctg(-1-√3)+πn,n∈Z