Разложим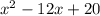 
на множители с группировки.
Разложи выражение на множители путем группировки. Сначала выражение необходимо переписать в следующем виде: x^2 +ax+bx+20. Чтобы найти a и b, настрой систему для решения.
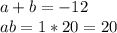
Поскольку ab положительное, a и b имеют одинаковый знак. Так как a+b отрицательный, a и b являются отрицательными. Перечисли все такие пары, содержащие 20 продукта.
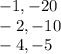
Вычисли сумму для каждой пары.
−1−20=−21
−2−10=−12
−4−5=−9
Решение — это пара значений, сумма которых равна −12.
Перепишите 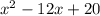как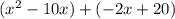 
Вынесите за скобки общий член x−10, используя свойство дистрибутивности.
Получим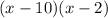 
a x^{2} +bx + c = a(x - x_{1} )(x - x_{2} )
Где, x_{1} и x_{2} - корни уравнения
a) x^{2} +14x + 48 = 0
D = 14^{2} - 4*1*48 = 4 = 2^{2}
x_{1} = \frac{-14+2}{2} = -6
x_{2} = \frac{-14-2}{2} = 8
x^{2} +14x + 48 = (x - (-6))(x - (-8)) = (x+6)(x+8)
b) 25 x^{2} -10x-12 =0
D = (-10)^{2} - 4*25*(-12) = 1300= (10 \sqrt{13}) ^{2}
x_{1} = \frac{-(-10 +10 \sqrt{13})}{2*25} = \frac{1}{5} + \frac{1}{5} \sqrt{13}
x_{2} = \frac{-(-10 -10 \sqrt{13})}{2*25} = \frac{1}{5} - \frac{1}{5} \sqrt{13}
Подставляем в формулу:
25 x^{2} -10x-12 = 25(x - ( \frac{1}{5} + \frac{1}{5} \sqrt{13} ))(x - (\frac{1}{5} - \frac{1}{5} \sqrt{13}) ) = (25x -5 + 5 \sqrt{13} )(x - (\frac{1}{5} - \frac{1}{5} \sqrt{13}) ) = (25x -5 + 5 \sqrt{13} )(x -\frac{1}{5} + \frac{1}{5} \sqrt{13}))
ответ:
решение:
\frac{2}{x - 2}
x−2
2
= x - 1 | x - 2 ≠ 0 | одз: x ≠ 2
2 = (x - 1)(x - 2)
2 - (x - 1)(x - 2) = 0
2 - (x² - 2x - x + 2) = 0
2 - (x² - 3x + 2) = 0
2 - x² + 3x - 2 = 0
- x² + 3x = 0
- x(x - 3) = 0
x = 0
x = 3
ответ: 0 и 3
графическое решение:
y = \frac{2}{x - 2}
x−2
2
- гипербола (|, |||)
x -3 -2 -1 1 2 3
y -0.4 -0.5 -2/3 -2 - 2
y = x - 1 - прямая
x -2 2
y -3 1
далее построить график и найти пересечение