1)
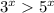
Так как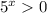 
при любых х, делим обе части неравенства на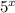 
⇒ 
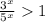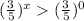
Показательная функция с основанием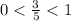 
убывает, то
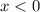
О т в е т.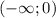 
2)
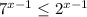
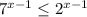
Так как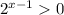 
при любых х, делим обе части неравенства на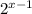 
⇒ 
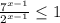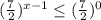
Показательная функция с основанием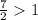 
возрастает, то
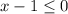
О т в е т. ![(-\infty;1]](/tpl/images/1361/5304/a162d.png)
3)
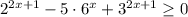
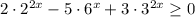
Так как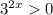 
при любых х, делим обе части неравенства на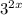 
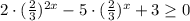
D=25-4·2·3=25-24=1
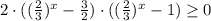
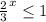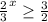
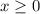или 
или 
О т в е т. ![(-\infty; -1]\cup [0;+\infty)](/tpl/images/1361/5304/edb57.png)
4)
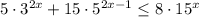
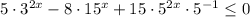
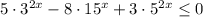
Так как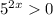 
при любых х, делим обе части неравенства на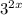
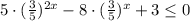
D=64-4·5·3=64-60=4
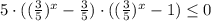
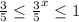
так как показательная функция с основанием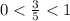 
убывающая, то
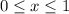
О т в е т. ![[0; 1]](/tpl/images/1361/5304/6a286.png)
Записываем площадь 1/2*a^2*V3/2=3*V3 (^2 читай "в квадрате", V - читай "корень квадратный").
Получаем a^2=12 => a=V12=2V3.
В равностороннем треугольнике медианы, высоты и биссектрисы совпадают и делятся в отношении 1:3. Точка их пересечения будет центром описанной вокруг треугольника окружности. Следовательно R окружности равен 1/3 высоты треугольника.
Найдем высоту. S=1/2a*h=3*V3 => 1/2*2V3*h=3*V3 => h=3
R=2/3y=2