Для разложения многочлена на множители найдем его корни (напомним, что корнями многочлена называются числа, которые превращают его в ).
Согласно следствию из теоремы Безу целые корни такого многочлена следует искать среди делителей свободного члена. Делителями числа являются числа Последовательно начиная подставлять их в указанной последовательности, убеждаемся, что одним из корней данного многочлена является число Это означает, что можно выделить линейный множитель, записав
Для нахождения выполним деление на в столбик (см. рисунок). Получаем в частном квадратный трехчлен корни которого легко найти с теоремы Виета. Сумма корней должна быть равна а их произведение — Легко подобрать такую пару чисел: и Тогда а исходный многочлен раскладывается на множители следующим :
1) Если это прямоугольник (длина и ширина), то S0=a*b; S=1,2a*1,1b=1,32ab=1,32*S0 Площадь увеличится на 32%. Если же это треугольник, то речь идёт о основании и высоте. S0=a*h/2; S=1,2a*1,1h/2=1,32*S0 Увеличение все равно на 32% 2) a+b=56; a/3=b/4 4a=3(56-a); 7a=3*56=7*24 a=24; b=56-a=56-24=32 3) (4^6*9^5+6^9*120)/(8^4*3^12-6^11)= (2^12*3^10+2^9*3^9*2^3*3*5)/ (2^12*3^12-2^11*3^11)= (2^10*3^10*(4+4*5))/(2^11*3^11*(6-1)= 24/(6*5)=4/5=0,8 4) Было х яиц, взяли х/2, осталось тоже х/2. Второй раз взяли х/4, осталось х/4. Третий раз взяли х/8, осталось х/8, и это было 10 яиц. x/8=10; x=80 яиц было в корзине. Если же брали 4 раза половину остатка, то было 160.
Объяснение:
Для разложения многочлена на множители найдем его корни (напомним, что корнями многочлена называются числа, которые превращают его в
).
Согласно следствию из теоремы Безу целые корни такого многочлена следует искать среди делителей свободного члена. Делителями числа
являются числа 
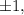
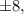
Последовательно начиная подставлять их в указанной последовательности, убеждаемся, что одним из корней данного многочлена является число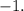 
Это означает, что можно выделить линейный множитель, записав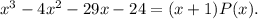 
Для нахождения
выполним деление 
на 
в столбик (см. рисунок). Получаем в частном квадратный трехчлен 
корни которого легко найти с теоремы Виета. Сумма корней должна быть равна 
а их произведение — 
Легко подобрать такую пару чисел: 
и 
Тогда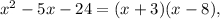 
а исходный многочлен раскладывается на множители следующим : 