Объяснение:
((a+7)\(a-7)-(a-7)\(a+7))\(14\(a^2-7a))
Приведем дроби в скобке к общему знаменателю a^2-49, домножив первую дробь на (a+7), а вторую на (a-7):
((a+7)^2-(a-7)^2)\(a^2-49)
По формуле разности квадратов:
((a+7-a+7)(a+7+a-7))\(a^2-49)
14*2a\a^2-49
28a\a^2-49
Представим деление одной дроби на другую умножением первой на перевернутую вторую:
(28a*(a^2-7a))\(14*(a^-49))
Вынесем в числителе "а" за скобку, а в знаменателе разложим скобку на множители:
(28a^2*(a-7))\(14(a-7)(a+7))
Сократим дробь:
2a^2\(x+7)
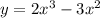
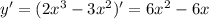
Необходимые условия экстремума:
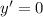
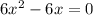
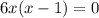
Имеем две критические (стационарные) точки: 
и 
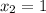
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой 
меняет знак с "+" на "–" (двигаясь в направлении увеличения 
), то — точка максимума, а если с "–" на "+" , то — точка минимума.
Из промежутка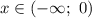 
выберем, например, 
и имеем: 
Из промежутка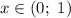 
выберем, например, 
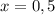и имеем: 
Имеем максимум в точке с абсциссой 
Из промежутка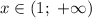 
выберем, например, 
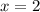и имеем: 
Имеем минимум в точке с абсциссой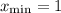 
ответ: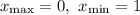 
,,,,,,,,,,,,,,,,,,,,,,,,