1) В таблице.
2)Координаты точки пересечения графиком оси Ох (0,5; 0);
Координаты точки пересечения графиком оси Оу (0; -2).
3)у= -3 при х= -0,25
4)Согласно графика, в 4 четверти лежит точка (0,3; -0,8)
Объяснение:
Задана функция y=4x-2
1) Постройте график функции.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у -6 -2 2
2) Найдите координаты точек с пересечения графика с осями координат.
а)график пересекает ось Ох при у=0.
y=4x-2
у=0
0=4х-2
-4х= -2
х= -2/-4
х= 0,5
Координаты точки пересечения графиком оси Ох (0,5; 0)
б)график пересекает ось Оу при х=0.
y=4x-2
х=0
у=0-2
у= -2
Координаты точки пересечения графиком оси Оу (0; -2)
3) Определите аргумент функции, если её значение ровно -3.
Найти значение х.
у= -3
y=4x-2
-3=4х-2
-4х= -2+3
-4х=1
х=1/-4
х= -0,25
у= -3 при х= -0,25
4) Укажите координаты точки на графике, которая лежит в 4 четверти(любой одной).
Согласно графика, в 4 четверти лежит точка (0,3; -0,8)
Для начала вспомним, что тупой угол - это угол с градусной мерой больше 90° и меньше 180°. Из одной точки можно пустить три луча, которые между собой образуют 3 тупых угла.
Пустим 4-й луч вблизи одного из трёх лучей, у нас добавится дополнительно 2 тупых угла. 5-й луч пустим вблизи второго из числа первых трёх, дополнительно образуются 3 тупых угла. Наконец, пускаем 6-й луч вблизи третьего, получив дополнительно 4 тупых угла. У нас будет получаться как бы три пучка близко расположенных лучей в каждом пучке.
Считаем сколько получилось тупых углов после добаления к первым трём лучам ещё трёх лучей. 3 луча было, плюс 2, плюс 3 и плюс 4, всего 12 лучей.
Итак, для 3-х лучей - 3 тупых угла; для 6 лучей - 12 тупых углов.
Рассуждаем аналогично, добавляя по очереди ещё 3 луча. Добавятся сначало 4 угла, затем 5 и, наконец, 6; т.е. всего добавится 15 тупых углов. А всего для 9 лучей будет 27 тупых углов.
Точно также, считая для 12 лучей, получим дополнительно 6+7+8 = 21 тупых угла, а всего - 48.
Можно было бы и далее продолжать таким но мы замечаем закономерность.
Пусть а1 = 3 - это первый член последовательности. Используя предыдущее значение (рекуррентно), можно вычислить следующее значение по формуле: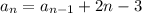
, где n - число лучей кратное 3.
Пробуем вычислить по этой формуле:
Итак, ответ найден. Для 27 лучей возможно максимум 243 тупых угла.
Так считать долго, можно увидеть формулу для прямого расчёта: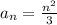
По этой формуле можно считать для любого количества лучей, кратное трём.
ответ:
объяснение:
начнем с того, что тупо списать я тебе не . я объясню пример а) в 563 номере, а остальные примеры - сам.
пример а, 563.
а) 3 - (
)
перед нами - линейное уравнение. алгоритм решения линейных уравнений:
1. если уравнение содержит скобки - раскрыть их.
2. если уравнение содержит дробь - домножить все члены уравнения на общий знаменатель.
3. перенести числа с буквой влево, а числа без буквы - вправо, изменив при этом знак на
4. произвести вычисления в левой и правой части.
итак, решаем:
уравнение содержит скобки - раскроем их.
если перед скобкой стоит знак минус, то при раскрытии этих скобок знак в скобке изменяется на противоположный.
домножаем почленно уравнение на общий знаменатель 12.
3 * 12 = 36
12 и 3 сокращается, доп.множитель у x + 1 - 4
доп.множитель у 3 - x - 3, так как 12 и 4 сократится.
у нуля - 12.
получаем:
36 - 4(x + 1) - 3(3 - x) = 0
раскрываем скобки:
36 - 4x -4 - 9 + 3x = 0
переносим вправо числа без буквы, изменив знаки чисел на противоположный:
имеем:
-4x + 3x = 0 + 9 + 4 - 36
-x = -23
теперь чтобы найти неизвестный множитель, -23 делим на -1 и получаем 23.