Практически тангенс возрастает везде, от минус бесконечности до плюс бесконечности. Только у тебя нюанс: cos2x не может быть равен нулю, иначе знаменатель занулится. А когда косинус 2х равен нулю? Это когда 2х равно пи/2 + пи*n Следовательно х в твоём случае не может быть равен пи/4 + пи/2*n (где n - ну ты понял, любое целое число).
Итого, ответ: y=tg(2x) возрастает на всём множестве х, за исключением точек х = пи/4 + пи/2*n, потому что в этих точках данная функция не существует - то есть имеет разрыв.
Объяснение:
1) Приводишь к общему знаменателю и при этом выполняется:
6х - 1 ≠ 0
х ≠ 1/6
(x+2)(6x-1) = 15
6x^2-x+12x-2-15 = 0
6x^2+11x-17 = 0
D = b^2-4ac
D = 11^2-4*6*(-17) = 121+408 = 529
x1 = (-b+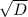 )/2a = (-11+23)/2*6 = 12/12 = 1
)/2a = (-11+23)/2*6 = 12/12 = 1
x2 = (-b-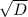 )/2a = (-11-23)/2*6 = -34/12 = -17/6
)/2a = (-11-23)/2*6 = -34/12 = -17/6
ответ: 1; -17/6
2) Чтобы найти точку пересечения двух графиков достаточно их приравнять и решить уравнение, т.е.:
2/x = x-1
2/x - x + 1 = 0
-x^2+x+2 = 0 Домножим на (-1):
x^2 -x -2 =0
по т. Виета:
x1+x2 = 1
x1*x2 = -2
x1= 2 x2= -1
Если x = 2, то у = 1
Если х = -1, то у = -2
ответ: (2;1) и (-1;-2)