Найдем, какую часть бассейна сможет наполнить каждая из труб за один час.
В условии задачи сказано, что первая труба может наполнить бассейн за 3 часа, а вторая труба наполняет весь бассейн за 2 часа, следовательно, за 1 час первая труба сможет наполнить 1/3 часть бассейна, а вторая труба сможет наполнить 1/2 часть бассейна.
Тогда, при совместной работе две трубы за 1 час смогут наполнить 1/2 + 1/3 = 3/6 + 2/6 = 5/6 частей бассейна, а весь бассейн наполнят за 6/5 ч , что в минутах составляет (6/5) * 60 = 6 * 60 / 5 = 6 * 12 = 72 мин.
ответ: за 72 минуты.
Наиболее сложное решение:
Пусть x - количество бензина в первой бочке, а y - во второй. По условию задачи составим систему уравнений:
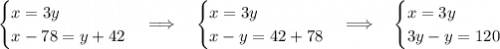
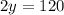
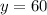 (л) - бензина во второй бочке
(л) - бензина во второй бочке
60 · 3 = 180 (л) - в первой бочке
Решение через уравнение (рационально):
Пусть x - количество бензина во второй бочке, тогда в первой - 3x. По условии задачи составляем уравнение:
3x - 78 = x + 42
3x - x = 42 + 78
2x = 120
x = 60 (л) - во второй бочке
60 · 3 = 180 (л) - в первой бочке
ответ: в первой бочке 180 л бензина, во второй - 60 л.
Задача может быть простой, даже несмотря на тему (здесь нельзя решить сложнее, чем в первом варианте)
ответ: 280 км
Объяснение:
пусть собственная скорость катера х км/ч, тогда
х+3 км/ч - скорость катера по течению реки
х-3 км/ч - скорость катера против течения реки
5*(x+3) - расстояние между двумя пунктами
5,6*(x-3) - расстояние между двумя пунктами
так как они равны, составим и решим уравнение
5,6*(x-3)=5*(x+3)
5,6х-16,8=5х+15
5,6х-5х=15+16,8
0,6х=31,8
х=31,8:0,6
х=53
5*(53+3)=280 км
или 5,6*(53-3)=280 км
ответ:280 км