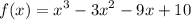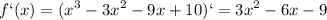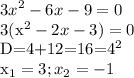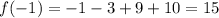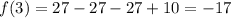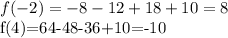![\int\limits {\frac{x^2}{\sqrt[4]{5-x^3} } } \, dx \\5-x^3=t-\frac{dt}{dx} =-3x^2-dx=-\frac{1}{3x^2} dt\\-\frac{1}{3} \int\limits {\frac{1}{\sqrt[4]{t} } } \, dt=-\frac{4\sqrt[4]{t^3} }{9}=-\frac{4\sqrt[4]{(5-x^3)^3} }{9}+C](/tpl/images/1011/7370/0b50b.png)
В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про бросание игральных костей и задачи о подбрасывании монет.
Перейдем еще к одному типу задач: про стрелков, которые делают выстрелы по целям (или мишеням), причем вероятности попаданий для каждого стрелка обычно заданы, а нужно найти вероятность ровно одного попадания, или не более двух попаданий, или всех трех и так далее, в зависимости от конкретной задачи.
Основной метод решения подобных задач - использование теорем о сложении и умножении вероятностей, который мы и разберем на примерах ниже. А перед примерами вы найдете онлайн калькулятор, который решить подобные задачи буквально в один клик! Удобно решать самому? Посмотрите видеоурок и скачайте бесплатный шаблон Excel для решения задач о выстрелах
Объяснение: