Объяснение:
у=-1/2х^2+х-1
Коэффициент перед х² отрицательный,значит ветви параболы направлены вниз. Число по модулю меньше 1. значит парабола "шире" параболы Х².Парабола имеет максимум.находим точки на оси Х.
у=0=-1/2х^2+х-1 *2
0=-х²+2х-2 ищем корни (-2±√(4-4*(-1)(-2))/(2*(-1)) =(-2±√(-4))/(-2)корней нет. Значит парабола целиком ниже оси Х.
Х вершины равен -в/2а=-1/(-1)=1
У вершины равен У=-1/2+1-1 =-1/2
(1;-1/2) вершина.
Строим таблицу х -1 0 1 2 3
у -2,5 -1 -0,5 -1 -2,5
Точка пересечения с осью У при Х=0 у= 0+0-1 =-1 (0;-1)
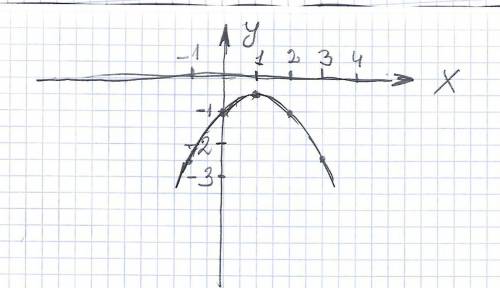
Теперь наносим эти точки на оси координат и соединяем плавной кривой. Свойства. Возрастает при х∠1 ,убывает при 1∠х .
отрицательна при всех значениях Х. вершина-точка максимума.
в первом номере мы можем подставлять вместо Х только те числа, при которых
х-5≥0
х≥5, значит можно брать только икс равный 5 и любое число больше 5. записываем это х∈[5;+∞) поставили квадратную скобку, потому что само число 5 тоже входит в область определения, и потому что стоит знак не просто >, а ≥ ( есть равно)
2. Во втором примере дробь. Значит можно брать только те иксы, при которых знаменатель не равен 0, так как на 0 делить нельзя. Найдем чему не должен равняться икс, чтобы х(х+2)≠0, значит х≠0 или х≠-2
все остальные числа можно подставлять в эту дробь, тогда область определения это х∈(-∞;-2)U(-2;0)U(0;+∞)
скобка круглая, потому что -2 и 0 не входят в число решений, а
U-знак объединения
3. в третьем примере нет никаких ограничений, вместо икс можно подставить любое число х∈(-∞;+∞)