34/56
Объяснение:
Чтобы три случайных числа a, b, c являлись сторонами треугольника нужно выполнение условий:
a+b>c
a+c>b
b+c>a
Найдем все удачные исходы:
При первом выпадении на кубике "1":
{1,1,1}, {1,2,2}, {1,3,3}, {1,4,4}, {1,5,5}, {1,6,6} - 6 исходов.
При первом выпадении на кубике "2":
{2,2,2}, {2,2,3}, {2,3,3}, {2,3,4}, {2,4,4}, {2,4,5}, {2,5,5}, {2,5,6}, {2,6,6} - 9 исходов.
При первом выпадении на кубике "3":
{3,3,3}, {3,3,4}, {3,3,5}, {3,4,4}, {3,4,5}, {3,4,6}, {3,5,5}, {3,5,6}, {3,6,6} - 9 исходов.
При первом выпадении на кубике "4":
{4,4,4}, {4,4,5}, {4,4,6}, {4,5,5}, {4,5,6}, {4,6,6} - 6 исходов.
При первом выпадении на кубике "5":
{5,5,5}, {5,5,6}, {5,6,6} - 3 исхода.
При первом выпадении на кубике "6":
{6,6,6} - 1 исход.
Всего успешных исходов N1 = 6+9+9+6+3+1 = 34
Общее число исходов равно числу сочетаний с повторениями:
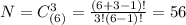
Искомая вероятность:
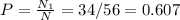
Объяснение:
9 вариантов каждого разряда, в котором не содержится цифра 1, за исключением первого ( в этом разряде не может быть 0, поэтому 8)
количество вариантов можно посчитать по формуле:
то же самое количество для чисел, которые не содержат любую другую цифру (кроме 0), так же и для 9ти
А количество чисел которые содержат хотя бы одну 9ку, нужно исключить из общего количества вариантов 10тизначных чисел те которые не содержат 9ку: