Объяснение:
1) Коэффициент при старшей степени (x^2) положительный, соответственно, ветви параболы направлены вверх
2) Чтобы уравнение имело 2 различных корня, дискриминант должен быть больше 0 (если дискриминант равен 0, то ответом являются 2 одинаковых корня; если дискриминант меньше 0, то корней на множестве действительных чисел нет)
D=b^2-4ac=(a-5)^2-4*1*9=a^2-10a+25-36=a^2-10a-11
a^2-10a-11>0
Найдем нули:
a^2-10a-11=0
a1=-1
a2=11
3) Выражение можно разложить на множители по формуле a(x-x1)(x-x2)
1*(a+1)(a-11)
(a+1)(a-11)>0
Расставим на числовой оси эти точки (выколотые) и знаки, получим ответ
a∈(-∝;-1)U(11;+∝)
ответ: a∈(-∝;-1)U(11;+∝)
Объяснение:
Для того чтобы показать, что число является составным достаточно показать, что оно у него есть делители помимо 1 и самого себя. Для начала надо понять на какое число заканчивается 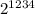 . Для этого нужно понять на какую цифру заканчиваются степени двойки:
. Для этого нужно понять на какую цифру заканчиваются степени двойки:
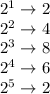
Таким образом последняя цифра в степенях двойки может быть только из множества {2, 4, 8, 6}, которое будет циклически повторяться. Дальше надо понять остаток от деления 1234 на 4. 1234 : 4 = 308 и остаток 2. Значит последния цифра у нас совершит 308 полных циклов и еще 2 шага. Таким образом число 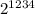 заканчивается на цифру 4. Следовательно
заканчивается на цифру 4. Следовательно 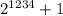 заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.
заканчивается на цифру 5, а значит это число делится на 5 и как факт является составным.
1)
Функция представлена произведением переменной на синус от экспоненты (сложная функция)
2)
Функция представлена произведение, поэтому дифференцируем по правилу дифференцирования произведения:
3)
Данная функция – разница двух других сложных функций.