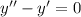
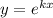, получим характеристическое уравнение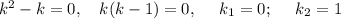
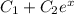- общее решение однородного уравнения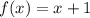
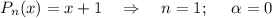
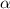с корнями характеристического уравнения, и принимая во внимания что n=1, частное решение будем искать в виде: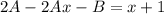
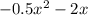
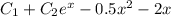
В решении.
Объяснение:
Если сторону квадрата уменьшить на 4 дм, то получится квадрат, площадь которого на 72 дм² меньше площади данного. Найдите исходную сторону квадрата.
х - исходная сторона квадрата.
х - 4 - уменьшенная сторона квадрата.
х² - площадь исходного квадрата.
(х - 4)² - площадь уменьшенного квадрата.
По условию задачи уравнение:
х² - (х - 4)² = 72
х² - (х² - 8х + 16) = 72
х² - х² + 8х - 16 = 72
8х = 72 + 16
8х = 88
х = 11 (дм) - исходная сторона квадрата.
Проверка:
11² - (11 - 4)² = 11² - 7² = 121 - 49 = 72 (дм)², верно.
Объяснение:
1) a(a + b) - b(a - b) = a^2 + b^2
а²+ab-ab+b²= a^2 + b^2
а²+b²= a^2 + b^2
2) b(a - b) + b(b + c) = b(a + b) - b(b – с).
Преобразуем левую часть
b(a - b) + b(b + c)=ab-b²+b²+bc=ab+bc=b(a+c)
Преобразуем правую часть
b(a + b) - b(b – с)=ab+b²-b²+bc=ab+bc=b(a+c)
Левая часть равна правой части