Возьмём за х км- расстояние, которое первый пешеход не дошёл до пункта N.
7+х км- расстояние, которое 2 пешеход не дошёл до пункта M.
Так как скорость равна отношению пути к времени, можно составить уравнения скоростей 1 и 2 пешеходов.
(38-х)/7 (км/ч)- скорость первого пешехода. (38-7-х)/7; (31-х)/7 (км/ч)- скорость второго пешехода.
Общий путь, пройденный пешеходами за одно и то же время двигаясь одновременно навстречу друг другу, равен произведению скорости сближения на время.
S(общее за 4 часа пути)= V(сближения)*t, где t=4часа, S=38-2=36км, V(сближения)=V1+V2.
Составляем уравнение:
((38-х)/7) +((31-х)/7)=9
умножим все члены уравнения на 7;
38-х+31-х=63;
2х=69-63;
х=3.
3 км- расстояние, которое не первый пешеход не дошёл до пункта N.
Значит скорость 1 пешехода равна (38-3)/7=35/7=5 км/ч.
А скорость 2 пешехода равна (31-3)/7=28/7=4 км/ч.
ответ: 4 км/ч; 5 км/ч.
При умножении любого числа на 0 мы получаем 0 !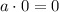 !
!
Поэтому, если задано уравнение, где в левой части стоит произведение каких-то выражений, а в правой части записан 0, то его очень легко решать, так как произведение равно нулю, когда какой-либо из множителей равен 0.
(х-4)(х-5)(х-6)=0 , если либо (х-4)=0, либо (х-5)=0 , либо (х-6)=0 .
То есть либо х=4 , либо х=5 , либо х=6 .
Значит мы получили три значения переменной "х", при которых левая часть обратиться в 0 . Это и есть корни уравнения.
Проверим, подставим вместо "х" значение 4, получим
(4-4)(4-5)(4-6)=0*(-1)*(-2)=0 .
х=5: (4-5)(5-5)(5-6)=(-1)*0*(-1)=0 ,
х=6: (6-4)(6-5)(6-6)=2*1*0=0 .
ответ: х₁=4 , х₂=5 , х₃=6 .