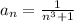Примем работу за 1. х часов надо первому, у часов надо второму. первый за час сделает 1/х часть работы, второй 1/у. Вместе за 6 часов они сделают (1/х + 1/у)*6 или всю работу; уравнение (1/х + 1/у)*6=1 за 6 часов первый сделает 6/х часть работы, второй за 4 часа 4/у часть работы, вместе 6/х + 4/у или 0,8 работы (80%); уравнение 6/х + 4/у=0,8. объединим в систему: 6/х + 6/у =1 6/х +4/у=0,8 вычтем второе уравнение из первого 2/у=0,2 у=10 (часов) подставим в первое уравнение и найдем х 6/х + 6/10=1 6/х=4/10 х=15 (часов) ответ: первому надо 15 ч, второму - 10 ч.
Примем работу за 1. х часов надо первому, у часов надо второму. первый за час сделает 1/х часть работы, второй 1/у. Вместе за 6 часов они сделают (1/х + 1/у)*6 или всю работу; уравнение (1/х + 1/у)*6=1 за 6 часов первый сделает 6/х часть работы, второй за 4 часа 4/у часть работы, вместе 6/х + 4/у или 0,8 работы (80%); уравнение 6/х + 4/у=0,8. объединим в систему: 6/х + 6/у =1 6/х +4/у=0,8 вычтем второе уравнение из первого 2/у=0,2 у=10 (часов) подставим в первое уравнение и найдем х 6/х + 6/10=1 6/х=4/10 х=15 (часов) ответ: первому надо 15 ч, второму - 10 ч.
a)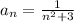
b)