ответ:Для того, чтобы представить выражение 4x^2 + y^2 + 4xy в виде квадрата двучлена мы применим формулу сокращенного умножения квадрат суммы.
Итак, вспомним прежде всего формулу квадрат суммы:
(a + b)^2 = a^2 + 2ab + b^2.
Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе, плюс квадрат второго выражения.
Но прежде чем применить формулу преобразуем выражение к виду:
4x^2 + y^2 + 4xy = 4x^2 + 4xy + y^2 = (2x)^2 + 2 * 2x * y + y^2 = (2x + y)^2.
Объяснение:
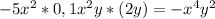; коэффициент - число (- 1); степень одночлена равна 6.
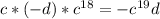; коэффициент - число (-1); степень одночлена равна 20
Объяснение:
Локальный экстремум ищем по первой производной.
y(x) = - x/(x² + 484)² - функция.
Находим корни у производной.
х² = 484
х = √484 = ± 22 - точки локального экстремума.
Рисунок с графиком функции в приложении.
Ymax(-22) = 0.0227
Ymin(22) = - 0.0227
Минимум при х = 22 - ответ.