Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
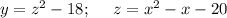
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
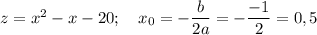- координата вершины
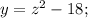z = 0 - координата вершины параболы
x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
35 км/ч
Объяснение:
Дано:
S₁ = 35 км
S₂ = 34 км
t = 2 ч
Vр = 1 км/ч
V - ?
1)
Заметим, что собственная скорость лодки равна скорости ее движения по озеру:
V₁ = V
Время, затраченное на движение по озеру:
t₁ = S₁ / V₁
или
t₁ = S₁ / V.
2)
Время, затраченное на движение по реке.
Заметим, что река впадает в озеро, а это значит, что лодка двигалась против течения: V₂ = V - Vp
t₂ = S₂ / V₂ или
t₂ = S₂ / (V - Vp)
3)
Общее время движения:
t = t₁ + t₂
или
t = S₁ / V₁ + S₂ / (V - Vp)
Подставляем данные и решаем уравнение:
2 = 35 / V + 34 / (V - 1)
2·V·(V-1) = 35·(V-1) + 34·V
2·V² - 2·V = 35·V - 35 +34·V
2·V² - 71·V + 35 = 0
Решая это квадратное уравнение, получаем:
V = (71-69)/4 = 0,5 км/ч (слишком маленькая скорость...)
V = (71+69)/4 = 35 км/ч
1/(x + y) + 1/(x - y) = 6 (1)
6/(x + y) - 1/(x - y) = 1 (2)
x ≠ y
x ≠ -y
складываем (1) и (2)
1/(x + y) + 1/(x - y) + 6/(x + y) - 1/(x - y) = 6 + 1
7/(x + y) = 7
x + y = 1
умножаем (1) на 6 и вычитаем (2)
6/(x + y) + 6/(x - y) = 36
6/(x + y) + 6/(x - y) - (6/(x + y) - 1/(x - y)) = 36 - 1
7/(x - y) = 35
x - y = 1/5
получили новую систему
x + y = 1
x - y = 1/5
2х = 6/5
x = 3/5
2y = 4/5
y = 2/5
ответ {3/5 2/5}