∀a ∈ ℝ: {a} ∈ [0; 1) ⇒ {x} - 1 ∈ [-1; 0).
∀a ∈ ℝ: [a] ∈ ℤ ⇒ [x] + ... + [x²⁰⁰³] ∈ ℤ.
Но [x] + ... + [x²⁰⁰³] = {x} - 1. Значит, {x} - 1 ∈ ℤ ∩ [-1; 0), то есть {x} - 1 = -1, или {x} = 0 ⇔ x ∈ ℤ.
Теперь переформулируем задачу.
Найдите все целые решения уравнения x²⁰⁰³ + ... + x + 1 = 0.
По следствию из теоремы Безу целые корни многочлена должны являться делителями свободного члена. В нашем случае свободный член - 1. У него два делителя: 1 и -1. Очевидно, что 1²⁰⁰³ + ... + 1 + 1 ≠ 0, а (-1)²⁰⁰³ + ... + (-1) + 1 = 0. Значит, имеем корень, равный -1. Других целых решений, как оговаривалось ранее, нет.
ответ: x = -1.
Объяснение: 2x²-8x+c = 0.
Имеем квадратное уравнение, где с - некоторое произвольное число (параметр), поэтому при разных значениях с уравнение может как иметь корни, так и не иметь. Поэтому нужно решить уравнения для всех возможных значений с.
Найдем дискриминант: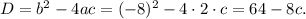
Рассмотрим 3 различных случая:
1) D < 0. Если D < 0, то уравнение не имеет решений. Найдем значения с, при которых дискриминант отрицателен: 64 - 8c < 0; 8c > 64 ⇔ c > 8. При таких значениях с корней у нас не будет вообще.
2) D = 0. Если D = 0, то уравнение имеет единственное решение: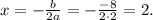
Найдем значение с, при котором дискриминант равен 0: 64 - 8c = 8 ⇔ c = 8. При таком значении параметра имеем один корень - х = 2.
3) D > 0. Если D > 0, то уравнение имеет два различных корня, которые находятся по общей формуле: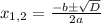
. Выразим каждый из корней:
Аналогично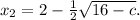
Найдем значения с, при которых дискриминант положителен: 64 - 8с > 0; 8с < 64 ⇔ c < 8. При таких значениях параметра у нас будут два корня: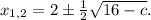
ОТВЕТ: если с < 8, то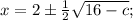
если с = 8, то х = 2; если с > 8, то корней нет.