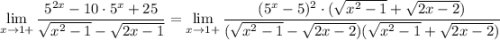
![=\displaystyle \lim_{x \to 1+}\frac{25(5^{x-1}-1)^2\cdot (\sqrt{x^2-1}+\sqrt{2x-2})}{x^2-1-2x+2}=\\ \\ \\ =\lim_{x \to 1+}\frac{25(5^{x-1}-1)^2\cdot (\sqrt{x^2-1}+\sqrt{2x-2})}{(x-1)^2}=\left[\begin{array}{ccc}\displaystyle \lim_{x \to 0}\frac{a^x-1}{x}=\ln a\end{array}\right] =\\ \\ \\ =\lim_{x \to 1+}25(\ln 5)^2\cdot (\sqrt{x^2-1}+\sqrt{2x-2})=25\ln^25\cdot 0=0](/tpl/images/1021/0841/efc6f.png)
Дан ромб ABCD: AC = 2√3 и BD = 2 — диагонали. Диагонали точкой пересечения делятся пополам и перпендикулярны друг другу, тогда:
OA = OC = AC/2 = 2√3/2 = √3;
OB = OD = BD/2 = 2/2 = 1;
∠AOB = ∠BOC = ∠COD = ∠DOA = 90°.
Таким образом, диагонали делят ромб ABCD на 4 равных прямоугольных треугольника.
1. Рассмотрим △AOB: ∠AOB = 90°, OA = √3 и OB = 1 — катеты.
Тангенсом острого угла прямоугольного треугольника является отношение длины катета, противолежащего данному углу, к длина катета, прилежащего к данному углу.
Найдем тангенс ∠OAB:
tg∠OAB = OB/OA = 1/√3 = 1/√3 * √3/√3 = (1 * √3)/(√3)² = √3/3.
∠OAB = 30°.
2. По теореме о сумме углов треугольника:
∠AOB + ∠OAB + ∠ABO = 180°;
90° + 30° + ∠ABO = 180°;
∠ABO = 180° - 120°;
∠ABO = 60°.
3. Диагонали ромба являются биссектрисами его углов, тогда:
∠A = 2 * ∠OAB = 2 * 30° = 60°;
∠B = 2 * ∠ABO = 2 * 60° = 120°.
Так как противолежащие углы ромба равны, то:
∠A = ∠C = 60°;
∠B = ∠D = 120°.
ответ: ∠A = 60°, ∠B = 120°, ∠C = 60°, ∠D = 120°.