2) как известно все углы прямоугольника прямые. <А=<В=<С=<D=90`
С диагоналей разбивает их на прямоугольные треугольники ACD и АВС .
угол ACD равен 60' по условии задачи . А угол D =90' => угол CAD=30'. Итак все углы треугольника АСD известны теперь переходим на треугольник АВО. Т .к. угол А =90' в угол САD=30' угол ВАО=60' . Угол ВЕА =90' в угол BAO=60' значит угол ABE=30'=ЕВО.
По условии задачи ОЕ=4см . По условии прямоугольного треугольника :если один из углов треугольника равен 30' то противоположный катет равен половине гипотенузы. В нашем случае катет лежащий противоположно углу ЕВО=30' это ОЕ=4см
Отсюда следует что гипотенуза ВО=2ОЕ=2×4=8 . Так как точка О середина отрезка BD то ВD=2 ×BO=2×8=16
B прямоугольника диагонали равны значит диагональ АС=ВD= 16 см
Объяснение:
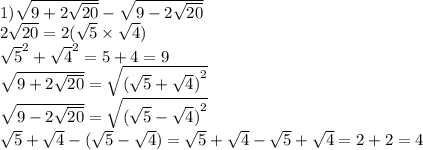
Дано:
АВСД - ромб
уг В = уг Д = 60*
АВ=ВС=СД=ДА= 20
АН высота
Найти:
ВН и НС ?
1) диагонали ромба пересекаются в т О. ВО=ОД. ВО - биссектриса уг В, след уг АВО= уг СВО = 60:2=30*. ( по свойству диаг ромба)
2) Рассм треуг АВО ( уг О=90*) В нем АВ=20, уг АВО = 30* След АО=10 ( по св-ву катета лежащего против угла в 30*).
3) АС= 2АО ( по св-ву ромба) АС=20
4) Рассм треуг ВАС - р/б ( АВ=АС=20) След АН - медиана ( по св-ву р/б треуг). Следовательно, ВН=НС=ВС/2. ВН=НС=20/2=10
ответ : длины отрезков на кот делит сторону ромба высота, опущенная из вершины тупого угла равны 10.
Решим квадратное уравнение:
2x^2 - 3x - 2 = 0
D = (-3)^2 - 4 * 2 * (-2) = 25
x1 = (- (-3) - √25)/(2 * 2) = (-6 - 5)/4 = -11/4 = -2,75
x2 = (-6 + 5)/4 = 0,25
По формуле:
ax^2 + bx + c = a(x - x1)(x - x2)
2x^2 - 3x - 2 = 2(x + 2,75)(x - 0,25)