применим метод прямоугольного треугольника. Сейчас я опишу его действие. Он позволяет вычислять точныее значения нетабличных углов. Построим прямоугольный треугольник. Пусть у нас угол α будет при стороне b. Пусть arccos 2/3 = α, тогда по определению арккосинуса cos α = 2/3. Видно, что нам надо найти tg 2α. Применим формулу тангенса двойного угла:
tg 2α = 2tg α / 1 - tg² a.
Отсюда следует, что нам нужно найти tga. tg α = sin α/cosα. Косинус мы знаем, надо найти синус.
cos α = b / c
b / c = 2/3
b = 2, c = 3
sin α = a / c
a = √(c² - b²) = √5
Отсюда sin α = √5 / 3
tg α = sin α / cosα = √5/3 : 2/3 = √5/2
Теперь осталось найти всего лишь tg 2α:
tg 2α = √5 / 1 - 5/4 = √5 : -1/4 = -4√5
Таким образом, tg 2α = tg(2arccos 2/3) = -4√5
ответ получен. Всё остальное делаем по аналогии. Рисунок сейчас приложу моих рассуждений
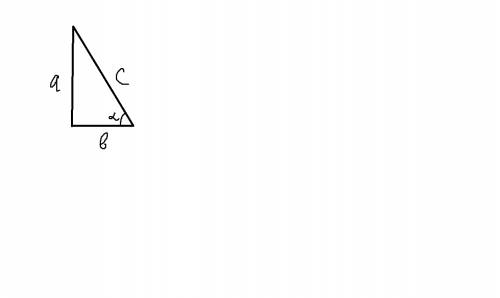
1) После раскрытия скобок выражение принимает вид:
Эта функция имеет 2 минимума:
1. (0,8; 1,8)
2. (10,2; -36).
2) Запишем пропорцию - a/b = c/d a = b + 6 c = d + 5
(b + 6) / b = (d + 5) / d Отсюда 6d = 5b d = 5b / 6
По условию a^2 + b^2 + c^2 + d^2 = 793
Подставив значения, получим - (b + 6)^2 + b^2 + (d + 5)^2 + d^2 = 793.
После раскрытия скобок - 2b^2 + 12b + 2d^2 + 10d + 61 = 793/
Заменив d = 5b / 6 и приведя к общему знаменателю, получим
72b^2 + 432b + 50b^2 + 300b = 26352 или 122b^2 + 732b - 26352 = 0
Корни этого уравнения равны -18 и 12. Отрицательное значение отбрасываем - b = 12.
а =12 + 6 = 18 - это первый член пропорции