Відповідь:
Шість головних діагоналей дорівнюють подвоєній стороні шестикутника.
Шість додаткових діагоналей дорівнюють стороні шестикутника помноженій на корень квадратний із трьох.
Пояснення:
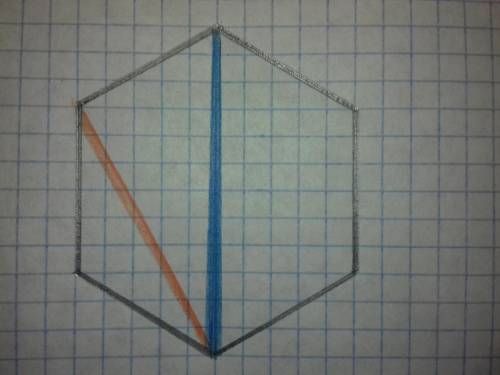
У правильному шестикутнику є шість головних діагоналей, що проходять крізь його геометричний центр ( центр описаної та вписаної окружності ), одна з них намальована синім кольором на малюнку. Довжина цієї діагоналі дорівнює подвоєній стороні шестикутника. Тому, що у правильному шестикутнику сторона дорівнює радіусу описаної окружності, а діагональ дорівнює двом радіусам.
Існує ще шість додадкових діагоналей, що не проходять крізь центр шестикутника, одна з таких діагоналей намальована червоним кольором на малюнку. Довжина такої діагоналі дорівнює стороні шестикутника помноженій на корень квадратний із трьох. Тому, що ця діагональ утворює рівнобічний трикутник з кутом при основі 30°, а основа трикутника дорівнює стороні шестикутника помноженій на 2 × cos (30°) = sqrt (3).
x ∈ (-∞, -1) ∪ (-1/3, 0] ∪ [4, +∞)
Объяснение:
находим ОДЗ x ∉ [ -1, -1/3 ] отсюда>>
область допустимых значений: x ∈ (-∞,-1) ∪ (-1/3, +∞)
Для а>1 выражение log a(x) ≥ log a(y) равно x≥y
4x^2 + 1 ≥ 3x^2 + 4x + 1
4x^2 ≥ 3x^2 + 4x
4x^2 - 3x^2 - 4x ≥ 0
x^2 - 4x ≥ 0
x ( x - 4 ) ≥ 0
возможны 2 случая когда произведение a*b будет ≥ 0.
(либо два отрицательных)
(либо два положительных)
Проверяем
x≥0 <=> x≥0 <=> x ∈ [4 , +∞ )
x-4≥0 x≥4
x ≤ 0 <=> x≤0 <=> x ∈ ( - ∞, 0 ]
x - 4 ≤0 x≤4
находим объединение для x ∈ ( - ∞, 0 ] и x ∈ [4 , +∞ ), получаем множество решений
МНОЖЕСТВО РЕШЕНИЙ x∈ (- ∞,0] ∪ [4, +∞) ,
ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ x ∈ (-∞,-1) ∪ (-1/3, +∞)
нахождение пересечения множеств решений и области допустимых значений
x ∈ (-∞, -1) ∪ (-1/3, 0] ∪ [4, +∞)
sinx=(корень2)/2 => x = PI/4
x = (-1)^n*PI/4 + PIn
n = - 2; x = PI/4 - 2PI = - 7PI/4
n = - 1; x = -PI/4 - PI = - 5PI/4
n = 0; x = PI/4
n = 1; x = -PI/4 + PI = 3PI/4
n - 2; x = PI/4 + 2PI = 9PI/4 находится за пределами области значения Х.
n = -2. -1. 0 . 1. 4 корня.