1) Разность арифметической прогрессии: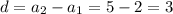 
. Тогда по формуле n-го члена арифметической прогрессии, найдем четырнадцатый член:
2) Пятый член: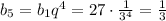 
Сумма четырех первых членов геометрической прогрессии:
3) Знаменатель прогрессии: 
Сумма бесконечно убывающей геометрической прогрессии:
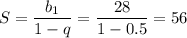
4) Здесь в условии опечатка, скорее всего d=-0.5, а если так как есть то задача решения не имеет.
ответ: 7
5) 
- геометрическая прогрессии
![b_4=b_1q^3~~\Leftrightarrow~~ q=\sqrt[3]{\dfrac{b_4}{b_1}}=\sqrt[3]{\dfrac{20}{2.5}}=2](/tpl/images/0269/0920/8578b.png)
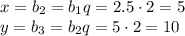
6) 6; 12; .... ; 96; 102; 108; .... ;198 - последовательность чисел, кратных 6.
Посчитаем сколько таких чисел:
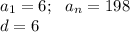
Сумма первых 33 членов а.п.: 
Нам нужно найти сумму всех натуральных чисел превышающих 100 и меньших 200 , которые кратны 6
, значит найдем сумму не превышающих 100 и отнимем от суммы не превышающих 200
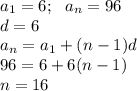
Искомая сумма: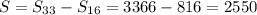 
Сумма квадратов 1 + 25 + 16 = 42 - делится на 3, но не делится на 9.
Или 847 = 11*77
8^2 + 4^2 + 7^2 = 64 + 16 + 49 = 129 - делится на 3, но не делится на 9.
Нашел простым подбором, это было нетрудно.
А вот найти все решения через решение уравнений - трудно.
Если число 100a + 10b + c, то должна выполняться одна из систем:
{ a + c = b
{ a^2 + b^2 + c^2 = 9k + 3
ИЛИ
{ a + c = b
{ a^2 + b^2 + c^2 = 9k + 6
ИЛИ
{ a + c = 11 + b
{ a^2 + b^2 + c^2 = 9k + 3
ИЛИ
{ a + c = 11 + b
{ a^2 + b^2 + c^2 = 9k + 6