1) смежные: ∠1 и ∠2
2) вертикальные: ∠1 и ∠3, ∠5 и ∠7
3) внутренние односторонние:∠4 и ∠5
4) соответственные: ∠4 и ∠8, ∠3 и ∠7
5) внутренние накрест лежащие: нет среди предложенных углов.
6) внешние накрест лежащие: ∠1 и ∠7, ∠2 и ∠8
Объяснение:
∠4 и ∠8 - 4 соответственные
∠1 и ∠2 - 1 смежные
∠4 и ∠5 - 3 внутренние односторонние
∠1 и ∠3 - 2 вертикальные
∠1 и ∠7 - 6 внешние накрест лежащие
∠3 и ∠7 - 4 соответственные
∠2 и ∠8 - 6 внешние накрест лежащие
∠5 и ∠7 - 2 вертикальные
∠4 и ∠6 и ∠3 и ∠5 - внутренние накрест лежащие
х=(-1) и х=(-5.5)
Решение: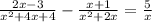
Формула сокращённого умножения:
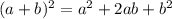
По этой формуле х²+4х+4 мы можем записать как (х+2)². Также вынесем х в знаменателе второй дроби.
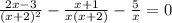
Приведём дроби к общему знаменателю:
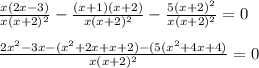
Если дробь равна нулю, числитель равен нулю, знаменатель - не равен нулю.
ОДЗ:
х(х+2)² ≠ 0
х≠0 и (х+2)²≠0
х≠0 и х+2≠0
х≠0 и х≠(-2)
Прировняем числитель дроби к нулю:
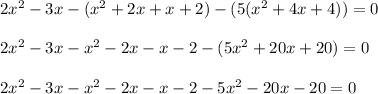
Приведём подобные слагаемые:
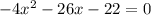
Умножим уравнение на (-1):
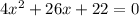
Имеем квадратное уравнение. Решим по дискриминанту.
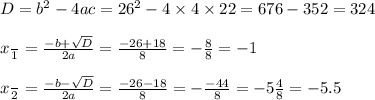
Учёв ОДЗ, имеем два решения: х=(-1) и х=(-5.5).
ответ:
рассматриваемая тема является одним из разделов курса и начала анализа. она имеет широкое применение в таких науках как , и др. аппарат этой темы при вычислении определенных и неопределенных интегралов и пределов функций, при доказательстве неравенств, в исследовании функций в высшей . кроме того, данная тема имеет свою , ей занимались и занимаются такие ученые как г. лейбниц, ж. лагранж, и. ньютон, г. галилея, р. декарта. подробнее остановимся на изложении аспекта темы. термин «производная» является буквальным переводом на французкого слова derive, которое ввел в 1797 г. ж. лагранж (1736-1813); он же ввел современные обозначения . такое название отражает смысл понятия: функция происходит из , является производным от . и. ньютон называл производную функцией флюксией, а саму функцию- флюентой. г. лейбнич говорил о дифференциальном отношении и обозначал производную как . символ лейбниц выбрал для обозначения дифференциала функции . дифференциальное исчисление создано ньютоном и лейбницем сравнительно недавно, в конце xvii столетия. тем более поразительно, что за долго до этого архимед не только решил на построение касательной к такой сложной кривой, как спираль, но и сумел найти максимум функции . в xvii в. на основе учения г. галилея о движении активно развивалась кинематическая концепция производной. эта тема интересна и мне. цель моей работы - расширить свой кругозор и научиться решать по данной теме. чтобы достигнуть цели, мне пришлось решить следующие исследовательские . подобрать и изучить материал по этой теме. из изученного материала выбрать главное. систематизировать основной материал в форме реферативно-поисковой работы. научиться решать по теме. составить свои по данной теме и решить их. подобрать и разработать наглядно-иллюстративный материал по данной теме. глава 1. понятия необходимые для решения с производной 1.1определение производной пусть мы имеем функцию y=f(x), определенную в некотором промежутке. при каждом значении аргумента x из этого промежутка функция y=f(x) имеет определенное значение. пусть аргумент x получил некоторое (положительное или отрицательное- безразлично) приращение δx. тогда функция y получит некоторое приращение δy. таким образом: при значении аргумента x будем иметь y=f(x), при значении аргумента x+ δx будем иметь y+δy=f(x+δx). найдем приращение функции δy: δy=f(x+δx)- f(x) (2) составим отношение приращения функции к приращению аргумента: . найдем предел этого отношения при . если этот предел существует, то его называют производной данной функции f(x) и обозначают . таким образом, по определению, или . определение 1. производной данной функции y=f(x) по аргументу x называется предел отношения приращения функции δy к приращению аргумента δx, когда последнее произвольным образом стремится к нулю. заметим, что в общем случае для каждого значения x производная имеет определенное значение, т.е. производная является также функцией от x. наряду с обозначением для производной употребляются и другие обозначения, например , . конкретное значение производной при обозначается или . операция нахождения производной от функции f(x) называется дифференцированием
источник: