Объяснение:
Решение задачи:
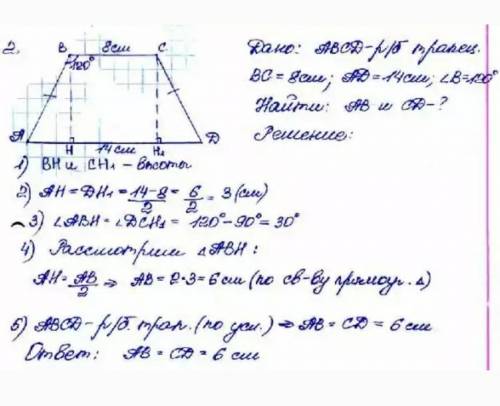
Рассмотрим равнобедренную трапецию АВСД. С углов В и с опустим перпендикуляры ВК и СМ на основание АД. Образовался прямоугольник КВСМ и два прямоугольных треугольника АВК и МСД. Рассмотрим треугольник АВК. Угол АКВ прямой и равен 90 градусов. Угол АВК равен 120 - 90 = 30 градусов. Сторона Ак равна (14 - 8) / 2 = 3 сантиметра. Катет прямоугольного треугольника АВК лежит против угла в 30 градусов, а значит гипотенуза АВ равна 2 * 3 = 6 сантиметров.
ответ: Боковые стороны трапеции равны 6 сантиметров.
-4a²+4ab-b²=-(4a²-4ab+b²)=-(2a-b)²
x²-y²-6x+9=x²-6x+9-y²=(x-3)²-y²=(x-3-y)(x-3+y)
(a+3)²-27=a²+6a-18 (у вас здесь, видимо, опечатка, т.к. разложение на множители не получается)
(a-7)³+8=(a+9)(a²+12a+39)
Уравнения:
16х²-25=0 (скорее всего здесь должен быть минус, т.к. если плюс - то решений нет)
(4х-5)(4х+5)=0
4х-5=0
4х+5=0
4х=5
4х=-5
х=1.25
х=-1.25
ответ: х1=1.25, х2=-1.25
(3х-5)²-16=0
(3х-5-16)(3х-5+16)=0
(3х-21)(3х+11)=0
3х-21=0
3х+11=0
3х=21
3х=-11
х=7
х=-1/3
ответ: х1=7, х2=-1/3
Убедительная присвойте этот ответ в качестве лучшего!