D(y)=R
Объяснение:
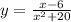
Для того, чтобы функция существовала, знаменатель должен быть не равен нулю.Найдем точки в которых знаменатель обращается в нуль
x²+20=0
x²=-20
x∈∅
Таких точек нет, значит область определения функции все рациональные числа
1) 8 < 2x+y < 30
2) 6 < xy < 48
3) -3 < x-y < 6
Объяснение:
3 < x < 8
2 < y < 6
1) 2x+y
сначала вычислим минимальный предел:
2*3+2=8;
затем максимальный:
8*3+6=30.
Получится 8 < 2x+y < 30
2) xy
сначала вычислим минимальный предел:
3*2=6;
затем максимальный:
8*6=48.
Получится 6 < xy < 48
3) x-y
Так как здесь присутствует вычитание. Сначала из меньшего значения x вычитаем большее значение y, так мы получим минимальный предел выражения x-y. Потом из большего значения x вычитаем меньшее значение y, так мы получим максимальный предел значения x-y.
сначала вычислим минимальный предел:
3-6=-3;
затем максимальный:
8-2=6.
Получится -3 < x-y < 6
Знаменатель дроби не должен равняться нулю, так как на ноль делить нельзя. Значит :
x² + 20 ≠ 0
x² ≠ - 20
Но x² ≥ 0 при любых действительных значениях x .
Значит областью определения являются все значения x ∈ R .