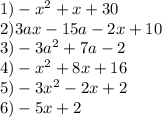
Відповідь:
Для вирішення цього завдання можна використати біноміальний розподіл.
Біноміальний розподіл характеризується двома параметрами: ймовірністю успіху в окремому експерименті (у випадку дослідження якості продукції - 0,95) та кількістю спроб (у випадку даного завдання - 160).
Формула для обчислення ймовірності успіху в певній кількості спроб у біноміальному розподілі виглядає так:
P(X = k) = C(n, k) * p^k * (1 - p)^(n - k),
де
P(X = k) - ймовірність, що точно k спроб з n будуть успішними,
C(n, k) - коефіцієнт біноміального коефіцієнту (кількість ів вибрати k спроб з n),
p - ймовірність успіху в окремому експерименті (у нашому випадку 0,95),
k - кількість успішних спроб,
n - загальна кількість спроб.
Застосуємо цю формулу для знаходження ймовірності того, що 152 з 160 товарів будуть відмінної якості:
P(X = 152) = C(160, 152) * 0,95^152 * (1 - 0,95)^(160 - 152).
Розрахуємо це значення:
P(X = 152) ≈ 0,0747
Отже, ймовірність того, що 152 з 160 товарів будуть відмінної якості, становить близько 0,0747 або 7,47%.
Пояснення: