х=t^2 2t^2-9t+4=0 a=2,b=-9,c=4 D=b^2-4ac=81-4*2*4=49>0-2 корня t1=-b+корень D/2a=9+корень 49/4=9+7/4=4 t2=-b-корень D/2a=9-корень 49/4=9-7/4=1/2 х^2=4 или х=2 х^2=1/2 или х=корень 1/2,-корень 1/2
1. нет; 2. 1) общего вида 2) общего вида 3) общего вида 3. 1) -1; 3 2) 1; -3 4) -1
Объяснение:
1. Если функция нечетная то произведение f(3)f(-3) не будет положительным.
2.
1)
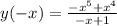
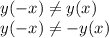
Это функция общего вида
2)
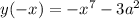
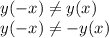
Это функция общего вида
3)
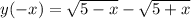
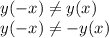
Это функция общего вида
3.
1)
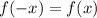
Значит
![min_{[2;4]}f(x)=min_{[-4;-2]}f(x)=-1\\max_{[2;4]}f(x)=max_{[-4;-2]}f(x)=3](/tpl/images/3904/3705/69e2d.png)
2)
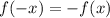
Значит
![min_{[2;4]}f(x)=-min_{[-4;-2]}f(x)=1\\max_{[2;4]}f(x)=-max_{[-4;-2]}f(x)=-3](/tpl/images/3904/3705/5cc0f.png)
4.
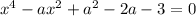
Это биквадратное уравнение. Делаем подстановку
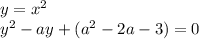
Уравнение будет иметь один корень, когда дискриминант равен 0
Но, поскольку х=±√у, то при любом положительном у мы получим два различных значения х. Одно значение х мы получим лишь в случае у=0. Тогда х=√0=0. Следовательно
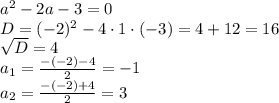
Делаем проверку:
1) а=-1
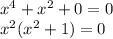
Имеется одно решение (т.к выражение в скобках никогда не будет равно 0)
2) а=3
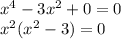
Здесь появляется второй корень. Значит, это значение не подходит.
Окончательно получаем решение: а=-1
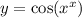
Мы видим, что данная функция является сложной, поэтому будем её дифференцировать как сложную.
Формула
d/dx( f(g(x)) ) = f'(g(x)) × g'(x), где в нашем случае f(x) = cos(x), а g(x) = x^x.
Для применения правила дифференцирования сложной функции, заменим x^x новой переменной t.
Дифференцируем
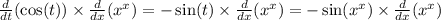
Для упрощения производной запишем х^х как e^( ln(x^x) ).
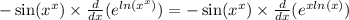
И опять сложная функция.
Дифференцируем её аналогично:
f(x) = e^x, g(x) = xln(x)
Заменим xln(x) перевенной k:
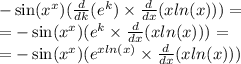
За правилом производной произведения имеем:
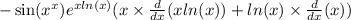
Вычисляем все производные и получаем:
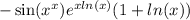
Это и есть ответ.
2*х^4-9*х^2+4=0
x^2=t, t>0
2*t^2-9*t+4=0
Получаем t=4, t=1/2. Находим x. x^2=4, т.е. x=2, x=-2. x^2=1/2, т.е. x=1/корень(2), x=-1/корень(2).
ответ: x=2, x=-2, x=1/корень(2), x=-1/корень(2).