1.
a)
x² + 4x + 10 ≥ 0
Рассмотрим функцию у = x² + 4x + 10.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 4x + 10 = 0
D = 16 - 40 = - 24 < 0
нулей нет, значит график не пересекает ось Ох.
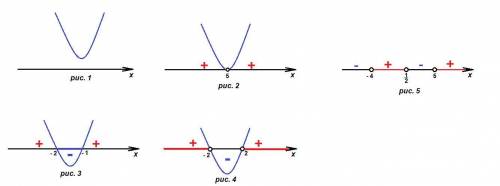
Схематически график изображен на рис. 1.
у > 0 при x ∈ (- ∞; + ∞)
ответ: 2) Решением неравенства является вся числовая прямая.
b)
- x² + 10x - 25 > 0 | · (- 1)
x² - 10x + 25 < 0
Рассмотрим функцию у = x² - 10x + 25.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 10x + 25 = 0
(x - 5)² = 0
x = 5
Схематически график изображен на рис. 2.
у < 0 при x ∈ {∅}
ответ: 1) Неравенство не имеет решений.
c)
x² + 3x + 2 ≤ 0
Рассмотрим функцию у = x² + 3x + 2.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 3x + 2 = 0
D = 9 - 8 = 1
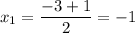
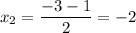
Схематически график изображен на рис. 3.
у ≤ 0 при x ∈ [- 2; - 1]
ответ: 4) Решением неравенства является закрытый промежуток.
d)
- x² + 4 < 0 | · (- 1)
x² - 4 > 0
Рассмотрим функцию у = x² - 4.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 4 = 0
x² = 4
x = ± 2
Схематически график изображен на рис. 4.
у > 0 при x ∈ (- ∞; - 2) ∪ (2; + ∞)
ответ: 6) Решением неравенства является объединение двух промежутков.
___________________________
2.
(x - a)(2x - 1)(x + b) > 0
x ∈(- 4; 1/2) ∪ (5; + ∞)
Решение неравенства показано на рис. 5.
Найдем нули функции у = (x - a)(2x - 1)(x + b).
(x - a)(2x - 1)(x + b) = 0
(x - a) = 0 или (2x - 1) = 0 или (x + b) = 0
x = a x = 1/2 x = - b
Из решения неравенства следует, что нулями являются числа - 4, 1/2 и 5. Значит
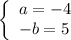 или
или 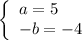
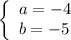 или
или 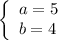
ответ: a = - 4, b = - 5 или a = 5, b = 4.
Объяснение:
1)Функция задана формулой у = 2х – 7
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
у = 2х – 7
Таблица:
х -1 0 1
у -9 -7 -5
Найдите значение функции, если значение аргумента равно -3.
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
у=2*(-3)-7= -6-7= -13
2)Функция задана формулой у = -4х – 8,5.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
у = -4х – 8,5
Таблица:
х -1 0 1
у -4,5 -8,5 -12,5
Найдите значение аргумента, при котором значение функции равно 3,5.
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у=3,5
3,5= -4х-8,5
4х= -8,5-3,5
4х= -12
х= -3
3) Постройте графики функций у = -5х +3 и у= -4.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
у = -5х +3
Таблица:
х -1 0 1
у 8 3 -2
График у= -4 представляет из себя прямую, параллельную оси Ох, проходящую через точку у= -4.
101 т кокосов и 43 т бананов.
Объяснение:
Чтобы вывезти 80 т кокосов, нужно собрать 80 т и еще
80*200 = 16000 кг = 16 т кокосов, то есть всего 80 + 16 = 96 т.
И еще 80*400 = 32000 кг = 32 т бананов.
Чтобы вывезти 10 т бананов, нужно собрать 10 т и еще
10*100 = 1000 кг = 1 т бананов, то есть всего 10 + 1 = 11 т.
И еще 10*500 = 5000 = 5 т кокосов.
Итого получается 96 + 5 = 101 т кокосов и 32 + 11 = 43 т бананов.