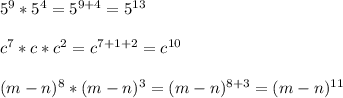
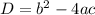(если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена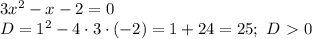
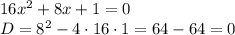
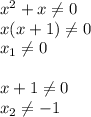
В решении.
Объяснение:
Решить уравнения:
1) 2х + 7/у = 11
7х + 2/у = 16
Умножить оба уравнения (все части) на у, чтобы избавиться от дробного выражения:
2ху + 7 = 11у
7ху + 2 = 16у
Умножить первое уравнение на -7, второе на 2, чтобы решить систему методом сложения:
-14ху -49 = -77у
14ху + 4 = 32у
Сложить уравнения:
-14ху+14ху-49+4 = -77у+32у
-45 = -45у
45у = 45
у = 1;
Теперь подставить значение у в любое уравнение системы и вычислить х:
2ху + 7 = 11у
2х = 11*1 - 7
2х = 4
х = 2;
Решение системы уравнений (2; 1).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
2) 12/х + 25/у = 7
6/х + 5/у = 2
Умножить оба уравнения (все части) на ху, чтобы избавиться от дробного выражения:
12у + 25х = 7ху
6у + 5х = 2ху
Умножить первое уравнение на -2, второе на 7, чтобы решить систему методом сложения:
-24у - 50х = -14ху
42у + 35х = 14ху
Сложить уравнения:
-24у + 42у -50х + 35х = -14ху + 14ху
18у - 15х = 0
-15х = -18у
15х = 18у
х = 18у/15
х = 1,2у;
Теперь подставить значение х в любое уравнение системы и вычислить у:
6у + 5х = 2ху
6у + 5*1,2у = 2у*1,2у
6у + 6у = 2,4у²
-2,4у² + 12у = 0/-1
2,4у² - 12у = 0
2,4у(у - 5) = 0
2,4у=0
у₁ = 0;
у - 5 = 0
у₂ = 5;
х = 1,2у;
х₁ = 1,2*0
х₁ = 0;
х₂ = 1,2*5
х₂ = 6.
По ОДЗ х и у не могут быть равны нулю.
Решение системы уравнений (6; 5).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
3) (х - 9)(х - 6)/(у + 8) = 0
(у + 8)(у - 8)/(х - 6) = 0
Умножить первое уравнение на (х + 8), а второе на (х -6), чтобы избавиться от дробного выражения:
(х - 9)(х - 6) = 0
(у + 8)(у - 8) = 0
Раскрыть скобки:
х² - 6х - 9х + 54 = 0
у² - 64 = 0
Привести подобные члены:
х² - 15х + 54 =0
у² - 64 = 0
Вычислить у из второго уравнения:
у² = 64
у₁,₂ = ±√64
у₁ = -8;
у₂ = 8;
х² - 15х + 54 =0, квадратное уравнение, ищем корни:
D=b²-4ac = 225-216=9 √D= 3
х₁=(-b-√D)/2a
х₁=(15-3)/2
х₁=12/2
х₁=6;
х₂=(-b+√D)/2a
х₂=(15+3)/2
х₂=18/2
х₂=9;
По ОДЗ х не может быть равен 6, а у не может быть равен -8.
Решение системы уравнений (9; 8).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.
