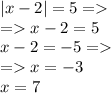
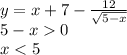
Пусть подмодульное выражение больше нуля:
x>0. Тогда функция приобретает вид
, при этом -1+3.5 x≠0, x≠2/7
Пусть теперь подмодульное выражение меньше нуля:
x<0. Тогда функция приобретает вид
, при этом -1-3.5 x≠0, x≠-2/7.
Построим график (см. приложенный файл) и отметим на нем выколотые точки: x≠-2/7 и x≠2/7
Очевидно, что прямая y=kx не будет иметь с графиком общих точек только в том случае, если будет проходить через выколотые точки. Определим угловой коэффициент k для случая x=-2/7 (соответствующее значение функции y = -3.5)
-3.5 = k*(-2/7), k = 49/4.
Определим угловой коэффициент k для случая x=2/7 (соответствующее значение функции y = -3.5)
-3.5 = k*(2/7), k = -49/4
ИЗВИНИТЕ НЕ МОГУ ПРИСЛАТЬ КАРТИНКУ.
b=24:100a
b=7+c
c=16:100a
7+16:100a=24:100a
16:100a+24:100a=7
40:100a=7
4:10a=7
a=7*4:100
a=2.8