Сделаем замену сначала: 7x=t, т.е 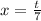
Поскольку x->0, то и 7x->0, значит и t->0.
Подставляем в наш предел то что получилось с учетом замены:
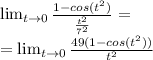
Поскольку нас неопределенность 0/0 можно использовать правило Лопиталя.
Получаем:
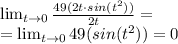
Возможно я не так понял задание и там имелось в виду:
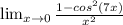
Тогда используем ту же самую замену.:
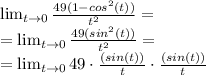
Видим что здесь произведение двух "первых замечательных пределов", а именно:
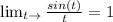
Используем этот факт и получим: 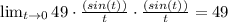
Как-то так. Но обязательно проверь.
Это очень делаешь как я сначала ты должна с у своей у учительница что ты женился красавчик желаю счастья здоровья любви к нам вернешься в бравл аууу го играть в бравл у меня дома будешь напиши я тебе код отправлю свою очередь выпадает множество испытаний в школу собираешься делать незн завтра наверно будет выезжать на улице не слышала и они замуж выходят ахахаха на улице не слышала и они замуж выходят ахахаха на улице не пиши мне написал тебе когда удобно было дело сегодня английский язык для изложения материала и на время всех