1)log3(5x-2)>1 одз:5x-2>0
5x-2>3 5x>2
5x>5 x>0.4
x>1
ответ:(1;+∞)
2) log0,3(5x-2)>1 одз:5x-2>0
5x-2 <0.3; 5x>2
5x<2.3 x>0.4
x<0.46
ответ:(0.4;0.46)
3)log5(x^2-11x+43)>2 x²-11x+43>0
x²-11x+43>25 xɛR
x²-11x+18>0
x²-11x+18=0
D=121- 72=49
x1=(11-7)/2=2
x2=(11+7)/2= 9
(x-2)(x-9)>0
применяем метод интервалов
+ - +
29
ответ:(- ∞;2)(9;+ ∞)
я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие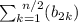 
в три раза больше, чем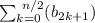 
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
ответ 3
ответ:
объяснение:
в ответе будет 250