Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру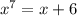 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
1. Будем доказывать методом математической индукции.
Проверяем истинность утверждения при n = 1:
а) 2*49 + 16 + 40 = 154 = 11*14 - делится на 11.
б) Предположим, что 2*7^(2k) + 16^k +8*5^k - делится на 11. Где k - произвольное натуральное число.
в) Докажем, что тогда при n = k+1 полученное выражение - тоже делится на 11:
Теперь четко видно что оба больших слагаемых делятся на 11:
первое - исходя из предположения, второе - имеет 11 как общий сомножитель для своих слагаемых.
Итак мы доказали , что если при произвольном n= k выражение делится на 11, то и при n = k+1 выражение делится на 11.
Значит исходное выражение делится на 11. что и требовалось доказать.
2)
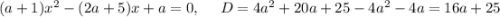
D>0 a>-25/16 a>-1,5625
Разбиваем ОДЗ на две части:
а) (-1; беск)
Первое из написанных неравенств верно. Проверим второе:
16a+25<16a^2+56a+49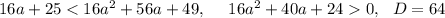
Корни -1; -1,5 Решение с учетом ОДЗ: (-1; беск)
б) (-1,5625; -1)
Правая чать на выбранной области - отрицательна, что недопустимо. Здесь решений нет.
ответ: (-1; бескон).
3.
ответ: 1