Question

80б. нужно решить уравнения пуьем выделения полного квадрата, а не дискриминантом. поменяли , голову ломаю. решите

Answer 1

Первый пример объясню поподробнее, чтобы было понятнее, как и зачем.

Объяснение: A) 2х² + 3х + 1 = 0.

Обе части разделим на 2, чтобы выделить "чистенький" квадрат икса: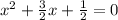  $x^2+\frac{3}{2}x+\frac{1}{2} =0$

Для того, чтобы решить выделением полного квадрата нужно представить левую часть в виде квадрата суммы. Одно число для этого - х - у нас уже есть. Ищем второе - пусть оно равно b. В нашем случае 3/2 х это по сути удвоенное произведение 2аb (a = x). Теперь мы можем найти b.

$\frac{3}{2} x=2xb;\Rightarrow \frac{3}{2} =2b\Rightarrow4b=3\Rightarrow b=\frac{3}{4}$.

До полного квадрата нам не хватает одного слагаемого -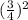 $(\frac{3}{4} )^2$. Чтобы "влепить" его в наше равенство, прибавим его к левой части. Однако нужно обязательно его вычесть, потому что нужно как-то компенсировать подобный переход.

Перепишем наше уравнение в следующем виде: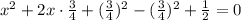 $x^2+2x\cdot\frac{3}{4} +(\frac{3}{4} )^2-(\frac{3}{4} )^2+\frac{1}{2} =0\\$.

Первые три слагаемые образуют квадрат суммы. Последние два перекинем вправо с противоположным знаком:

$(x+\frac{3}{4})^2=\frac{9}{16}-\frac{1}{2} \\(x+\frac{3}{4})^2=\frac{1}{16} \\x+\frac{3}{4} =\pm\frac{1}{4}\Rightarrow x=\pm\frac{1}{4} -\frac{3}{4} .\\x_1=\frac{1}{4} -\frac{3}{4} =-0,5\\x_2=-\frac{1}{4}-\frac{3}{4}=-1.$

Если решить дискриминантом, то можно легко убедиться в том, что корни найдены верно.

б) 2х² + x + 2 = 0;

$x^2+\frac{1}{2} x+1=0\\x^2+2\cdot\frac{1}{4}\cdot x+(\frac{1}{4})^2-(\frac{1}{4})^2+1=0\\(x+\frac{1}{4} )^2=\frac{1}{16} -1\\(x+\frac{1}{4})^2=-\frac{15}{16} .\\$

Квадрат вещественного числа не может быть отрицательным. Делаем вывод: корней уравнение не имеет.

В) 9x²+6x+1=0.

Чистый квадрат суммы: (3x+1)²=0;  3x+1 = 0 ⇒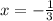 $x = -\frac{1}{3}$

Г) х² + 5x - 6 = 0

$x^2+2\cdot x\cdot\frac{5}{2} +(\frac{5}{2})^2-(\frac{5}{2})^2-6=0\\(x+\frac{5}{2})^2=\frac{25}{4} +6\\(x+\frac{5}{2})^2=\frac{49}{4} \\x+\frac{5}{2} =\pm\frac{7}{2} \\x=\pm\frac{7}{2} -\frac{5}{2} \\x_1=\frac{7}{2} -\frac{5}{2} =\frac{2}{2}=1\\x_2=-\frac{7}{2} -\frac{5}{2} =-\frac{12}{2}=-6$