Сначала раскроем скобки (чтобы не мучаться со взятием производной от произведений)
Получаем
(x+9)^2*(x+6)-5=(x^2+18x+81)(x+6)-5=x^3+24x^2+189x+481
Теперь возьмем производную от этой функции, получим:
f'(x)=3x^2+48x+189
Теперь найдем значение производной на границе нашего отрезка. Получаем:
f'(-10)=3*100-480+189=9
f'(-8)=3*64+48*(-8)+189=-3
Производная сменила знак, значит на это интервале она будет принимать значение 0 и в этой точке будет максимум функции, потому что если производная положительна, функция будет расти, если отрицательна, убывать. Значит функция будет расти от точки x до точки x1, где f'(x1)=0, а после нее будет убывать до точки где x=-8.
Найдем решения уравнения f'(x)=0, т.е
3x^2+48x+189=0
Обычно квадратное уравнение, найдем D
D=48^2-4*3*189= 2304-2268=36
Найдем решения уравнения:
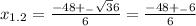
значит x1=-9, x2=-7, но т.к x2 не входит в отрезок [-10;-8], то нам подходит только одно решения x1=-9
ответ: Максимальное значение функции достигается в точке x=-9 и равно оно -5.
Примечание: Вообще можно заметить, что (x+9)^2 всегда положительное, а (x+6) будет всегда отрицательном на рассматриваемом промежутке. Значит чтобы функция достигла максимального значения необходимо просто сделать так, чтобы (x+9)^2*(x+6) было равно нулю. И здесь получаются 2 варианта:
1. х=-6 не подходит так как не пренадлежит отрезку [-10;-8]
2. x=-9, подходит.
Но этот метод будет не универсальным, а пригодным только для этого примера.
Пусть одна из сторон образовавшегося прямоугольника равна х см, то другая - (24-х) см. Площадь прямоугольника вычисляются по формуле S=a*b, то S=x*(24-x)
Зададим функцию S(x)=x*(24-x), исследуем ее и найдем при каком значении она принимает наибольшее значение. S(x)=x*(24-x)=24x-x^2
D(S)=(0; 24)
S'(x)=24-2x
S'(x)=0, 24-2x=0
-2x=-24
x=12
Найдем значение производной данной функции слева S'(11)=2>0 и справа S'(13)=-2<0 от значения х=12. Значение производной меняется с + на -, значит функция в точке х=12 достигает своего максимума. Площадь прямоугольника будет наибольшей, если стороны его 12см и 12 см, т.е - квадрат
1)1-22/100=78/100=39/50(чис.)-зменшили на 22%
2)39/50+39/50*1/4=39/50+39/200=39/40(чис.)-збільшили на 25%
3)1-39/40=1/40(чис.)-5,5
4)5.5:1/40=220-початкове число
ответ: 220.