Объяснение:
1) Приводишь к общему знаменателю и при этом выполняется:
6х - 1 ≠ 0
х ≠ 1/6
(x+2)(6x-1) = 15
6x^2-x+12x-2-15 = 0
6x^2+11x-17 = 0
D = b^2-4ac
D = 11^2-4*6*(-17) = 121+408 = 529
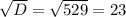
x1 = (-b+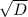
)/2a = (-11+23)/2*6 = 12/12 = 1
x2 = (-b-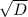)/2a = (-11-23)/2*6 = -34/12 = -17/6
ответ: 1; -17/6
2) Чтобы найти точку пересечения двух графиков достаточно их приравнять и решить уравнение, т.е.:
2/x = x-1
2/x - x + 1 = 0
-x^2+x+2 = 0 Домножим на (-1):
x^2 -x -2 =0
по т. Виета:
x1+x2 = 1
x1*x2 = -2
x1= 2 x2= -1
Если x = 2, то у = 1
Если х = -1, то у = -2
ответ: (2;1) и (-1;-2)
Объяснение:
1) Приводишь к общему знаменателю и при этом выполняется:
6х - 1 ≠ 0
х ≠ 1/6
(x+2)(6x-1) = 15
6x^2-x+12x-2-15 = 0
6x^2+11x-17 = 0
D = b^2-4ac
D = 11^2-4*6*(-17) = 121+408 = 529
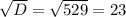
x1 = (-b+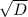)/2a = (-11+23)/2*6 = 12/12 = 1
x2 = (-b-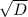)/2a = (-11-23)/2*6 = -34/12 = -17/6
ответ: 1; -17/6
2) Чтобы найти точку пересечения двух графиков достаточно их приравнять и решить уравнение, т.е.:
2/x = x-1
2/x - x + 1 = 0
-x^2+x+2 = 0 Домножим на (-1):
x^2 -x -2 =0
по т. Виета:
x1+x2 = 1
x1*x2 = -2
x1= 2 x2= -1
Если x = 2, то у = 1
Если х = -1, то у = -2
ответ: (2;1) и (-1;-2)
Е(g(x))=[7;+бесконечности)
Объяснение:
подкоренное выражение: у(х)=x^2+4x+53 - это парабола
перед х^2 находится коэффициент 1 —› ветви параболы направлены вверх, то есть наименьшее значение будет в вершине параболы: х(вершины)=-b/2a=-4/(2*1)=-2
y(вершины)=(-2)^2+4(-2)+53=4-8+53=49
то есть, наименьшее значение подкоренного выражения = 49, наиболее = бесконечность
тогда наименьшее значение g(x)=√y(x)=√49=7,
a наибольшее = бесконечность
значит Е(g(x))=[7;+бесконечности)