Объяснение:
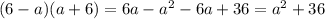
Рисуночек:
Аs1Х__s2__Б
вел-> 2ч<-пеш
v1 v2
{40км}
t>
<(t-7,5)
X - место встречи через 2 часа (ближе к городу пешехода, так как велосипедист движется быстрее)
s1 и s2 - отрывки пути по обе стороны места встречи (их сумма 40 км)
v1 - cкорость велосипедиста
v2 - скорость пешехода
t - время велосипедиста (ушедшее на 40 км)
t+7,5 - время пешехода (тоже на 40 км)
*Раз велосипедист потратил на 7,5 часов меньше, то пешеход разумеется на 7,5 часов больше. Можно и пеш=t, вел=t-7,5 , но так неудобнее*
За 2 часа они проехали суммарно все 40 км. (один сколько-то с одной стороны(s1), второй сколько-то с другой стороны(s2), итого весь путь, раз встретились)
*(1)* Стало быть:
s1(вел) + s2(пеш) = 40
Длинна пути (s) выражается через формулу скорости (v): v = s/t => s = v*t
*(2)* Вот и выразим:
s1 = v1*t и s2 = v2*(t+7,5)
*(3)* Исходя из (1) и (2):
v1*t + v2*(t+7,5) = 40
Велосипедист проехал второй отрывок(s2) за t-2 часа (s1 он проехал за 2ч).
Пешеход свой второй отрывок(s1) за t+7,5-2 часов т.е за t+5,5 часов (s2 он за 2ч)
*(4)* Значит:
s1 = v1 * 2 = v2 * (t+5,5)
s2 = v2 * 2 = v1 * (t-2)
*(5)* Соответственно получаем систему уравнений:
{v1 * 2 = v2 * (t+5,5)
{v2 * 2 = v1 * (t-2)
*(6)* Выражаем соотношения скоростей:
v1 * 2 = v2 * (t+5,5) => v1/v2 = 2/(t-2)
v2 * 2 = v1 * (t-2) => v1/v2 = (t+5,5)/2
*(7)* Объеденяем:
2/(t-2) = (t+5,5)/2
*(8)* Умножаем на 2(t-2) и открываем скобки:
4 = (t+5,5)(t-2)
4 = t^2 - 2t + 5,5t - 11
t^2 + 3,5t - 15 = 0
*(9)* Решаем квадратное уравнение:
t = -(3,5/2) +- sqrt((3,5/2)^2 -(-15)) = -1,75 +- sqrt(3,0625+15) = -1,75 +- 4,25
t1 = 2,5
t2 = -6 (лишнее)
Выходит, что у велосипедиста ушло 2,5ч на 40 км.
*(10)* Тогда у пешехода 2,5 + 7,5 = 10ч
*(11)* Их скорости соответственно:
v1 = 40км/2.5ч = 16 км/ч
v2 = 40км/10ч = 4 км/ч
***Проверка согласно тексту:
За 2 часа велосипедист проезжает 2*16 = 32 км,
а пешеход проходит 2*4 = 8 км
Итого 32 + 8 = 40, стало быть они действительно встретились через 2 часа после отправления.
У пешехода ушло на всю дистанцию 10ч, а у велосипедиста 2,5ч, что действительно на 7,5ч меньше чем у пешехода.
***ответ: Скорость велосипедиста 16 км/ч, скорость пешехода 4 км/ч.
1)
ОДЗ: 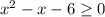 ⇒
⇒ 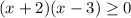 ⇒
⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
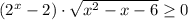 ⇔
⇔
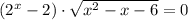 или
или 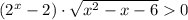
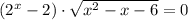 ⇒
⇒ 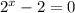 или
или 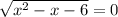 ⇒
⇒
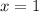 или
или  или
или 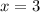
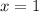 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 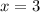
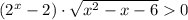 при
при ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
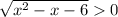 , тогда
, тогда 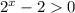 ⇒
⇒ 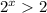 ⇒
⇒ 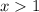
C учетом ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png) получаем ответ:
получаем ответ:
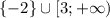
2)
ОДЗ: 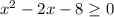 ⇒
⇒ 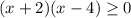 ⇒
⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
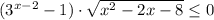 ⇔
⇔
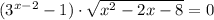 или
или 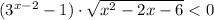
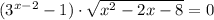 ⇒
⇒ 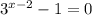 или
или 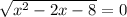 ⇒
⇒
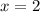 или
или  или
или 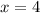
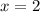 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 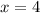
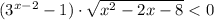 при
при ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
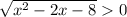 , тогда
, тогда 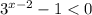 ⇒
⇒ 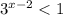 ⇒
⇒ 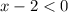
C учетом ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png) получаем ответ:
получаем ответ:
![(-\infty;-2]\cup \{2\}](/tpl/images/1361/5355/83f26.png)
3)
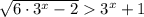
Так как 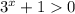 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
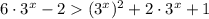
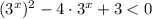
D=16-12=4
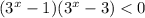
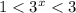
Показательная функция с основанием 3 возрастает
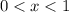
О т в е т. (0;1)
4)

Так как 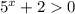 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
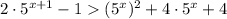
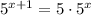
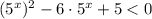
D=36-20=16
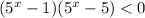
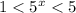
Показательная функция с основанием 5 возрастает
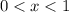
О т в е т. (0;1)
(6-a)(6+a)=36-a^2
Объяснение:
a^2-b^2=(a^2-b^2)(a^2+b^2)