(x,y)={(-5;-3), (-5;3), (3;-3), (3;3)}
Объяснение:
Заметим, что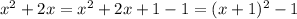 
, сделаем замену z=x+1,
получаем уравнение: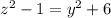 
, которое равносильно 
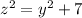, заметим, что выражение не зависит от знаков z и y, поэтому решим для целого неотрицательного z, если z>=5, то z^2-(z-1)^2=2z-1>=9, тогда заметим, что y<z, иначе 
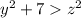, но тогда 
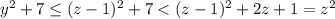. Таким образом решения есть при z<=4, теперь рассмотрим все случаи:
z=0 ⇒ y^2=-7 нет решений
z=1 ⇒ y^2=-6 нет решений
z=2 ⇒ y^2=-3 нет решений
z=3 ⇒ y^2= 2 нет решений
z-4 ⇒ y^2= 9 ⇒ y=3 или -3
Так как z может быть как положительным, так и отрицательным, то получается четыре пары решений (z,y):
(-4;-3), (-4;3), (4;-3), (4;3) Теперь вспомним, что x=z-1, откуда получается 4 пары (x,y):
(-5;-3), (-5;3), (3;-3), (3;3)
Объяснение:
Значение функции равно наибольшему целому числу, которое не больше соответствующего значения аргумента.
Тут интересно... Область определения данной функции - вся числовая ось x∈(-∞;+∞), но область допустимых значений функция имеет бесконечное количество точек разрыва (функция не непрерывная).
Рассмотрим промежуток для аргумента от 0 до 1. Возьмем любое число из этого промежутка, например 0,5. По условию - значение функции - целое число. Ближайшие целые числа это 0 и 1. Но, опять-таки по условию, это целое число не должно превышать значение аргумента, (y∈Z; y≤x; y≤0.5; y=0) а, значит, это число 0. Причем в т. х=1 значение функции не определено (т.е. здесь у функции точка разрыва).
Аналогично далее при x∈ [0;+∞):
x∈[1;2]; y∈Z; y≤2; y=1; в т. х=2 значение y не определено, и т.д.
Чуть сложнее при x∈[0;-∞)
Возьмем число из промежутка от 0 до -1. Например -0,999.
Ближайшие целые числа - это 0 и -1, но число, не большее x=-0.999 (y≤-0.999; y∈Z; y=-1) это -1 (число 0>-0.999). В точке х=0 значение y не определено (точка разрыва).
Данная функция называется "целая часть Х", записывается
y=[x]