1.
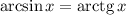
ОДЗ: арксинус определен при ![x\in[-1;\ 1]](/tpl/images/1421/5878/61ea0.png)
Найдем синус левой и правой части:
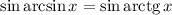
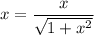
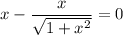
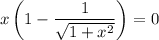
Уравнение распадается на два. Для первого уравнения получим:
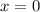
Решаем второе уравнение:
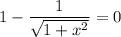
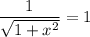
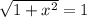
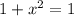
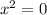
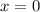
Таким образом, уравнение имеет единственный корень 0.
ответ: 0
2.
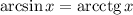
ОДЗ: арксинус определен при
Найдем синус левой и правой части:
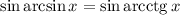
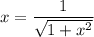
Так как в правой части стоит положительная величина, то и левая часть должна быть положительной, то есть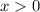 
.
Возведем в квадрат обе части:
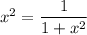
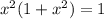
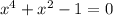
Решим биквадратное уравнение:
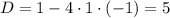
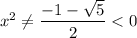
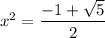
Находим х:
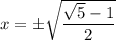
Однако, так как было выявлено ограничение 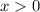, то отрицательный корень не попадает в ответ.
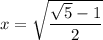
Оценив значение полученного корня, мы понимаем, что он удовлетворяет исходной ОДЗ:
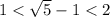
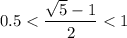
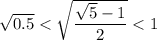
ответ: 
1. Итак, нам нужно понять какая эта функция! Для этого Вспомним, что функция f(x )-называется четной( нечетной), если для любого x∈D(f) и выполняется равенство f(x)=f(-x).
График четной функции симметричен относительно оси .
График нечетной функции симметричен относительно начала координат
Наш пример : y=x²-cos2x
Функция определенна при x∈(-∞;∞) , то есть f(-x)=(-x)²-cos2(-x)=-x²-cos2x=-(x²-cos2x)-функция является четной, т.к cosx-четная функция
2.Нам нужно сравнить два значения sin(-20°) V sin(-85)°, где V- знак сравнения ( птичкой называют)
Итак, sin(-20°)=sin(-10°)+sin30°≈0,1736+0,5≈-0,34
sin(-85°)=sin(-5°)-sin(90°)≈0,0872+1≈0,9999=грубо 1
sin(-20°) > sin(-85°). Есть еще более простой смотри поскольку числа не четные, пусть в место sin(-20°) будет sin(-30°)=-0,5 и sin(-85°) бусть будет sin(-90)=-1 и так -0,5>-1
ответ: 1) y=x²-cos2x- функция четная ; 2)sin(-20°) > sin(-85°)
Надеюсь, твой педагог не такая уш придирчивая. Удачи тебе!