Question

Решить. график-то построить могу, а, что означает найти y(-2), y(1), y (3)

Answer 1

Любая функция характеризуется значением у при определенных значениях х.

Значения х, называемые аргументом функции, - множество чисел, входящих в область определения данной функции.

Значения у, называемые значениями функции, - множество чисел, входящих в множество значений данной функции.

Очевидно, что выражение "найти у(-2)" означает нахождение значения функции (у) при х = -2

----------------------

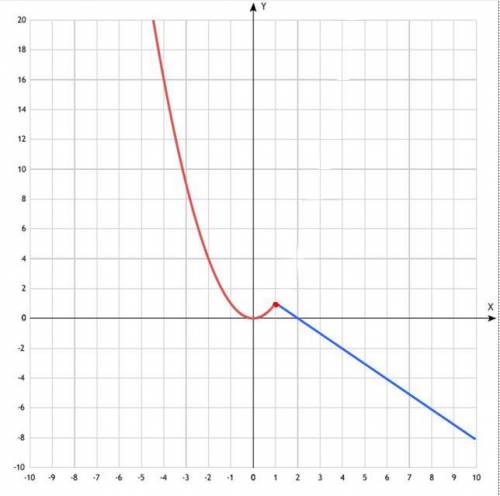
График функции состоит из двух частей:

красная ветвь соответствует уравнению у = х²,

синяя ветвь - уравнению у = 2 - х

Точка перехода графиков соответствует значению функции при х = 1

-----------------------

у(-2). Так как х = -2, то значение у (по условию) получаем из верхнего уравнения системы:

         у = х²

         у = (-2)² = 4

у(1). Так как второе уравнение системы определено для всех х > 1, то:

         у = х²

         у = 1² = 1

у(3). Так как значение х в данном случае больше 1, то используем для нахождения значения функции второе уравнение:

         у = 2 - х

         у = 2 - 3 = -1

Answer 2

Объяснение:

y(-2) - значение y при x = -2

y(1) - значение y при x = 1

y(3) - значение y при x = 3

На примере y(-2)

y(x) = y(-2), значит x = -2

По условию, -2 меньше, чем 1, значит решаем y(x) = x²

Подставляем наш x и решаем:

y(-2) = -2²

y(-2) = 4

Если скинешь свой график, на пальцах могу все объяснить сразу