Есть 12 вариантов выбора книг для покраски по количеству книг в каждом цвете (красный, зеленый, коричневый)
1 1 10
1 2 9
1 3 8
1 4 7
1 5 6
2 2 8
2 3 7
2 4 6
2 5 5
3 3 6
3 4 5
4 4 4
Им соответствуют количество вариантов выбора книг по их числу, например, первому, 12!/(10!*2!)*2!/(1!*1!)=66*2=132. Их надо посчитать.
И каждому набору соответствует число возможных перестановок по цветам. Если все числа в наборе разные, то 3!=6, если две одинаковые, до 3!/(2!*1!)=3, если все одинаковые (последний случай) , то 3!/(3!*0!)=1.
Затем количество вариантов выбора книг для каждого набора надо умножить на количество перестановок в наборе (то есть, для первого получится 132*3=396), и полученные числа сложить. Получится 519156.
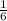
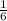 - 1 =
- 1 = 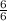 - 1 = 1-1=0
- 1 = 1-1=0
1) х'=1
2) (x²)'=2х
3) (x⁻¹)'=-1/х²
4)(x³/⁴)'=3/(4х¹/⁴)
5) (x-x¹⁰+x⁻¹)'=1-10х⁹-1/х²
6)(x⁶-0,1x¹⁰-x⁻¹)'=6х⁵-х⁹+1/х²
7) ((7/6)x⁶ - 0,01x¹⁰-2x⁻¹+12)'=7х⁵-0.1х⁹+2/х²
8) (√x)'=1/(2√х)
9) (3√x-14)'=3*(1/(2√х)=3/(2√х)
Производная константы везде равна нулю. Производная корня квадратного равна единице, деленной на два таких же корня.
Для остальных формула производной степенной функции использовалась. (xⁿ)'=n*x ⁿ ⁻¹