0,15 (x - 4) = 9,9 - 0,3 (x - 1)
0,15x - 0,6 = 9,9 - 0,3x + 0,3
0,15x + 0,3x = 9,9 + 0,3 + 0,6
0,45x = 10,8
x = 10,8 : 0,45 = 1080 : 45 = 24
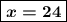
Проверка :
0,15 (24 - 4) = 9,9 - 0,3 (24 - 1)
0,15 · 20 = 9,9 - 0,3 · 23
3 = 9,9 - 6,9 = 3
-----------------------------------------------
1,6 (a - 4) - 0,6 = 3 (0,4a - 7)
1,6a - 6,4 - 0,6 = 1,2a - 21
1,6a - 1,2a = 6,4 + 0,6 - 21
0,4a = -14
a = -14 : 0,4 = - 140 : 4 = -35

Проверка :
1,6 (- 35 - 4) - 0,6 = 3 (0,4 · (-35) - 7)
1,6 · (-39) - 0,6 = 3 · (-14 - 7)
-62,4 - 0,6 = 3 · (-21)
-63 = -63
1)
Пусть 1 кг апельсинов стоит х рублей, а 1 кг лимонов у рублей. Тогда 7х+4у=700, а 5х-2у=160. Составим и решим систему уравнений:
7х+4у=700
5х-2у=160 |*2
7х+4у=700
10х-4у=320
17х=700+320
5х-2у=160
17х=1020
2у=5х-160
х=60
у=(5*60-160):2
х=60 руб цена 1 кг апельсинов
у=70 руб цена 1 кг лимонов
ответ 60 руб и 70 руб
2)
Пусть Х-ткань на 1плащ, а У- ткань на 1куртку. Система уравнений:
Х+3У=9
2Х+5У=16
Х=9-3У
2Х+5У=16
2(9-3У)+5У=16
18-6У+5У=16
-У=-2
У=2
Х=9-3*2=3
Проверка:
3+3*2=9
2*3+5*2=16 - решение верное.
ответ:на 1 плащ нужно 3м, на 1 куртку 2 м.
3)
Надо обозначить гантели через x, а гири через y, и составить систему уравнений:
2y+3x=47,
3y-6x=18;
2y+3x=47,
y=6+2x;
2(6+2x)+3x=47
12+4x+3x=47
7x=47-12
7x=35
x=5 (кг - вес гантели)
y=6+2x=6+10=16 (кг - вес гири)
ответ: гантели- 5кг, гири- 16кг.
4)
1. Обозначим кол-во в Первом ящике - х
во Втором ящике - у
Теперь составим уравнения, в зависимости из условий
х-45 = у+45
(х+20) = 3*(у-20)
Из первого выразим х и подставим во второе уравнение
х = у+90
(у+90+20) = 3*(у-20)
у+110 = 3у-60
2у = 170
у = 85 ябл - во втором ящике.
Теперь подставим у в уравнение с х и найдем х
х = у+90
х = 85+90 = 175 ябл - в первом ящике.
ответ : в первом ящике 175 яблок, а во втором - 85 яблок.
5)
6(х+у)=9(х-у)
3(х+у)+5(х-у)=76
2х+2у=3х-3у
3х+3у+5х-5у=76
5у=х
8х-2у=76
х=5у
4х-у=38
20у-у=38
19у=38
у=2
х=10
10 км/ч скорость катера
2 км/ч скорость течения
2) x² + 6x + 12 < 0
D = 6² - 4 * 12 = 36 - 48 = - 12 < 0
Дискриминант меньше нуля, старший коэффициент равен 1 > 0 , значит x² + 6x + 12 > 0 при любых действительных значениях "x" и меньше нуля быть не может .
Графиком является парабола, ветви которой направлены вверх, так как коэффициент при x² > 0 . Дискриминант < 0 , значит точек пересечения с осью OX нет . Следовательно x² + 6x + 12 > 0 при любых значениях x и меньше нуля быть не может.