Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
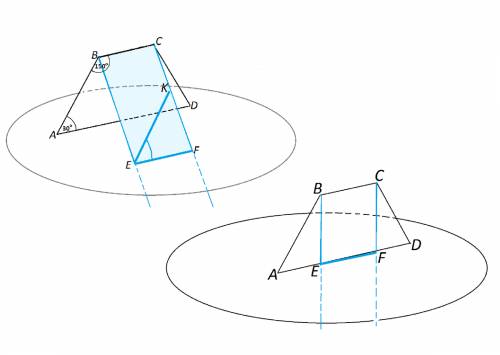
Сумма углов при боковой стороне трапеции 180°, следовательно, угол ВАD=180°-150°=30°.
Проведем в плоскости ВЕF прямую ЕК, параллельную АВ.
ЕК|║АВ; ЕF║АD Углы с соответственно параллельными сторонами равны, если они оба острые или оба тупые.⇒
∠FЕК=∠ВАD=30°
-----------
ВЕ и СF могут быть проведены в плоскости АВСD.
Тогда ЕD будет лежать на АD и в этом случае непараллельные прямые EF и АВ лежат в одной плоскости. Тогда АВ и EF пересекyтся.
1)
30% числа k = 0,3a
35% числа p = 0,35p
0,3k > 0,35p на 20
Первое уравнение:
0,3k - 0,35p = 20
2)
20% числа k = 0,2а
30% числа p = 0,3р
0,3р > 0,2k на 8
Второе уравнение:
0,2k + 8 = 0,3p
3)
Решаем систему.
{0,3k-0,35р = 20
{0,2k - 0,3р = - 8
Первое умножим на 2, а второе умножим на (-3)
{0,6k-0,7р = 40
{-0,6k+0,9р = 24
Сложим
0,6k-0,7р -0,6k+0,9р = 40+24
0,2р = 64
р = 64 : 0,2
р = 320
В первое уравнение 0,3k - 0,35p = 20 подставим р = 320.
0,3k - 0,35·320 = 20
0,3k - 112 = 20
0,3k = 112 + 20
0,3k = 132
k = 132 : 0,3
k = 440
ответ: k = 440;
р = 320.
Очевидно , что многочлен меньшей степени не может делится на больший , тогда n>=k .
Таким образом можно записать :
n=m*k +t t-остаток от деления n на k ( t=0,1,2,3k-1) ( t<k)
Запишем :
x^n-1 = x^(m*k+t) -1 = x^(m*k) * x^t -1 = x^(m*k) *x^t -x^t +x^t -1 =
= x^t*( x^(m*k) -1 ) +(x^t -1)
Многочлен : x^t*( x^(m*k) -1 ) делится на x^(k) -1 поскольку если поделить на x^k-1 многочлен в скобках получаем геометрическую прогрессию :
(x^(m*k) -1 )/(x^(k) -1) = 1+x^k +x^2k ... +x^k*(m-1)
Пусть остаток t≠0
Тогда поскольку t < k , то x^t -1 не делится на x^k -1 .
А значит очевидно,что весь многочлен :
x^t*( x^(m*k) -1 ) +(x^t -1) не делится на x^k -1
Таким образом x^n-1 делится на x^k-1 , только когда остаток t=0.
Иначе говоря n должно делится на k