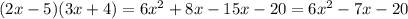
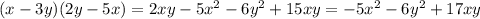
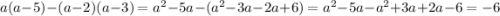
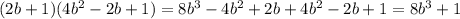
ответ:
объяснение:
дифференциальное уравнение — это уравнение, в которое входят функция и одна или несколько ее производных. в большинстве практических функции представляют собой величины, производные соответствуют скоростям изменения этих величин, а уравнение определяет связь между ними.
в данной статье рассмотрены методы решения некоторых типов обыкновенных дифференциальных уравнений, решения которых могут быть записаны в виде элементарных функций, то есть полиномиальных, экспоненциальных, логарифмических и тригонометрических, а также обратных им функций. многие из этих уравнений встречаются в реальной жизни, хотя большинство других дифференциальных уравнений нельзя решить данными , и для них ответ записывается в виде специальных функций или степенных рядов, либо находится численными .
для понимания данной статьи необходимо владеть дифференциальным и интегральным исчислением, а также иметь некоторое представление о частных производных. рекомендуется также знать основы линейной в применении к дифференциальным уравнениям, особенно к дифференциальным уравнениям второго порядка, хотя для их решения достаточно знания дифференциального и интегрального исчисления.
Держи, в последнем я так понял это квадрат.