Question

Какой угол составляет касательная к графику функции y=x^2+3x+4 в точке с абсциссой x0=-2,с положительным направлением оси ox? ​

Answer 1

$y = x^{2} + 3x + 4$

Найдем уравнение касательной, проходящей через точку с абсциссой $x_{0} = -2$

Для этого найдем производную данной функции:

$y' = (x^{2} + 3x + 4)' = 2x + 3$

Найдем значение функции в точке с абсциссой $x_{0} = -2$:

$y(-2) = (-2)^{2} + 3 \cdot (-2) + 4 = 4 - 6 + 4 = 2$

Найдем значение производной данной функции в точке с абсциссой $x_{0} = -2$:

$y'(-2) = 2 \cdot (-2)+ 3 = -4 + 3 = -1$

Уравнение касательной имеет вид:

$y = f'(x_{0})(x - x_{0}) + f(x_{0})$

Подставим значение $f'(x_{0}) = -1, \ f(x_{0}) = 2, \ x_{0} = -2$

$y = -(x + 2) + 2 = -x - 2 + 2 = -x$

Итак, уравнение касательной заданной функции: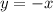 $y = -x$

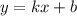Воспользуемся геометрическим смыслом касательной: коэффициент наклона $k$ касательной $y = kx + b$ численно равен тангенсу угла наклона 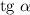$\text{tg} \ \alpha$  с положительным направлением оси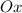 $Ox$

В найденной касательной коэффициент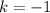 $k = -1$, следовательно, 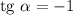$\text{tg} \ \alpha = -1$ при $\alpha = 135^{\circ}$ или $\alpha = \dfrac{3\pi }{4}$

ответ: $\alpha = 135^{\circ}$ или $\alpha = \dfrac{3\pi }{4}$