ответ: 128
Объяснение:
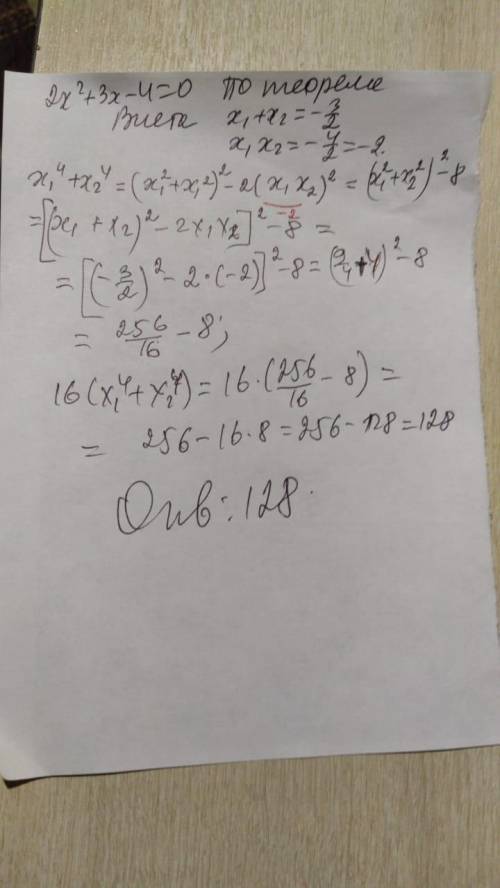
ответ:Для того, чтобы найти точки экстремума данной функции нужно найти в каких точках производная равна нулюразделим на 3Значит точки экстремума х=1 и х=-33) Чтобы определить какая из данных точек является точкой максимума, а какая точкой минимума необходимо рассмотреть значение производной на полученных интервалах___+-+ -3 1Если производная на промежутке принимает положительное значение то функция на данном промежутке возрастает, если отрицательное- то функция убываетЗначит на промежутке (-∞;-3) ∪ (1;+∞) функция возрастаетна промежутке (-3;1) убывает4) если до точки х= -3 функция возрастает а после точки -3 убывает, значит при х= -3 точка максимума функции если до точки х=1 функция убывает, а после точки х=1 возрастает то в точка х=1 точка минимуманайдем значение функции в этих точках
2x² + 3x - 4 = 0| : 2
x² + 1,5x - 2 = 0
По теореме Виета :
x₁ + x₂ = - 1,5
x₁ * x₂ = - 2
16(x₁⁴ + x₂⁴) = 16 [(x₁² + x₂²) - 2x₁²x₂²]² =16[(x₁ + x₂)² - 2x₁x₂]² - 2x₁²x₂² =
= 16[(- 1,5)² - 2 * (- 2)]² - 2 * (- 2)² = 16 (2,25 + 4)² - 8 = 16 * (6,25²- 8) = 497