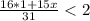
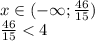то есть да может , так как 
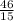ее целая часть равна 3 , а она натуральное число , и найдется набор таких чисел что среднее арифметическое будет меньше 2 , так как в условий не сказано что , сам набор может состоят так только из разных натуральных чисел. 
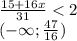, целая часть этого числа равна 
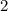, то есть не может , так как в сумме 
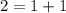, и по количеству в этом наборе минимальное есть 16 единиц . 
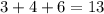так как мы ранее доказали что , есть не менее 16 единиц , и того 
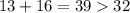что удовлетворяет условию .
Объяснение:
N^2+M^2=L^2 (*)
Пусть
N=3K+1
M=3J+1
L^2=9*(J^2+K^2)+6*(J+K)+2
Допустим J и K оба четные или оба нечетные. Тогда противоречие очевидно -слева число должно делиться на 4 , а справа не делится.
То же рассуждение проходит и для M=3J-1. Значит одно из чисел обязательно четное, другое нечетное. Но то же можно, стало быть , сказать и про М и Н. Но умножив оба таких числа на 2 мы не наруши свойство (*). Значит мы пришли к противоречию.