ответ: 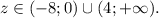
Объяснение:
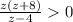
На каждом из интервалов (-∞; -8); (-8; 0); (0;4); (4; +∞) левая часть неравенства принимает значения только одного знака.
1. (-∞; -8) : z < 0; z+8 < 0; z-4 < 0; значит левая часть неравенства меньше 0;
2.(-8; 0): z < 0; z+8 > 0; z-4 < 0; значит левая часть неравенства больше 0;
3.(0; 4): z > 0; z+8 > 0; z-4 < 0; значит левая часть неравенства меньше 0;
4.(4; +∞): z > 0; z+8 > 0; z-4 > 0; значит левая часть неравенства больше 0;
Подходят только (-8; 0) и (4; +∞).
Найдём коэффициенты а, в, с
Подставим координаты точки А
-6 = а· 0² + в·0 + с → с = -6
Подставим координаты точки В
-9 = а·1² + в·1 - 6 → а + в = -3 (1)
Подставим координаты точки С
6 = а·6² + в·6 - 6 → 6а + в = 2 → в = 2 - 6а (2)
Подставим (2) а (1)
а + 2 - 6а = -3 → а = 1
Из (2) получим в = -4
Итак, мы получили уравнение параболы:
у = х² - 4х - 6
Абсцисса вершины параболы: m =-в/2а = 4 / 2 = 2
Ординату вершины параболы найдём,
подставив в уравнение параболы х = m = 2
у = 2² - 4 · 2 - 6 = -10
ответ: вершиной параболы является точка с координатами (2; -10)