Объяснение:
Для того, чтобы упростить выражение (b - 3)(b - 4) - (b + 4)2 мы откроем скобки, а затем выполним группировку и приведение подобных слагаемых.
Открывать скобки будем с правила умножения скобки на скобку, формулу сокращенного умножения квадрат суммы и правило открытия скобок перед которыми стоит минус.
Откроем скобки и получим выражение:
(b - 3)(b - 4) - (b + 4)2 = b2 - 4b - 3b + 12 - b2 - 8b - 16.
Выполним приведение подобных слагаемых.
b2 - 4b - 3b + 12 - b2 - 8b - 16 = b2 - b2 - 8b - 4b - 3b + 12 - 16 = -15b - 4.
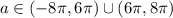
Объяснение:
Все ненулевые решения разбиваются на пары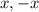 
. Чтобы у уравнения было 8 корней, у него должно быть ровно 4 положительных корня, и 0 не должен являться корнем. Дальше будем думать только о неотрицательных корнях.
Уравнение с косинусом легко решается:
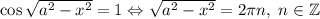
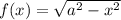— функция, которая убывает от 
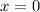до 
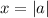, принимая все значения от 
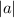до 0.
Значит, чтобы условие было выполнено, в промежуток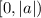 
должны попасть ровно 4 числа вида 
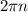. Понятно, что в промежуток попадут 0, 2π, 4π, 6π — и не попадут 8π и т.д.
Условие этого:
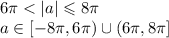
При этом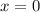 
не должен быть решением, поэтому 
, 
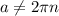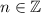. Это удалит из решения 
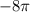и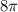 
.
x1=-2
x2=7
q=x1×x2. q=-14
-p=x1+x2. p=-5
(x+2)(x-7)=0
x2-5x-14=0
График квадратного трехчлена, является парабола. Так как коэффициент перед x^2 положителен, то ветви направлены вверх. Следовательно, у данной параболы, вершина является минимумом.
Найдем вершину:
x=-b/2a=-{-5}/{2} =2,5
y=2,5^2-5*2,5-14=6,25-12,5-14=-20,25
Следовательно, наименьшее значение квадратного трехчлена является -20,25, при x=2,5
найдем производную
x2-5x-14=0
f'x=2x-5
2x-5=0
x=2,5
Следовательно, критическая точка лишь одна. Узнаем, является ли она минимумом или максимумом.
Для этого, на координатной прямой, обозначим точку 2,5, и выделим 2 интервала с их знаками:
(-бесконечность; 2,5]
2х-5=>принимает отрицательное значение
[2,5; +бесконечность)
2х-5=>принимает положительное значение
Следовательно:
y(min)=y(2,5)=-20,25